Sign In
Sign Up
flag-us

Encontrando límites en gráficas

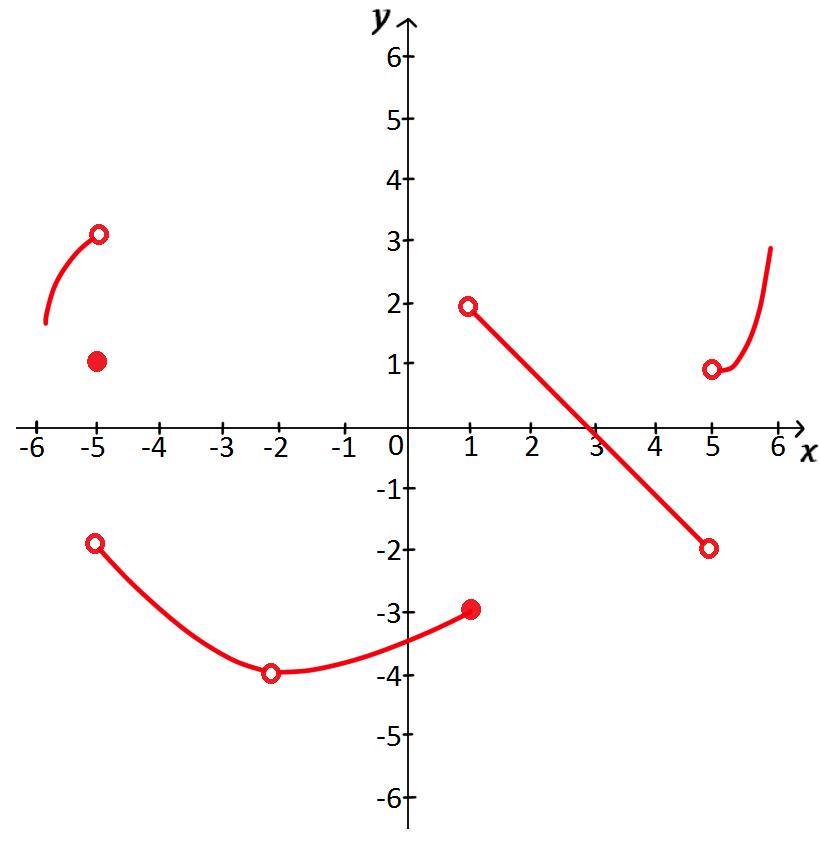
Now Playing:Es finding limits from graphs – Example 1a
Examples
  1. Para la función f que se muestra en la siguiente gráfica, encuentra lo siguiente:
    Finding limits from graphs

    1. limx→−5−f(x) lim_{x \to -5^-} f(x)
      limx→−5+f(x) lim_{x \to -5^+} f(x)
      limx→−5f(x) lim_{x \to -5} f(x)
      f(−5)f(-5)

    2. limx→−2−f(x) lim_{x \to -2^-} f(x)
      limx→−2+f(x) lim_{x \to -2^+} f(x)
      limx→−2f(x) lim_{x \to -2} f(x)
      f(−2)f(-2)

    3. limx→1−f(x) lim_{x \to 1^-} f(x)
      limx→1+f(x) lim_{x \to 1^+} f(x)
      limx→1f(x) lim_{x \to 1} f(x)
      f(1)f(1)

Encontrando límites en gráficas
Jump to:Notes
Notes
Un límite es un concepto fundamental para entender el cálculo, ya sea diferencial o integral.

En esta sección aprenderemos cómo obtener el límite de una función utilizando su gráfica además de aprender la diferencia entre los límites ordinarios (bilaterales) y los límites laterales.

DEFINICIÓN DE LÍMITES LATERALES:

Límite por la izquierda:  limx → m−f(x)=L \, lim_{x \, \to \, m^-} f(x) = L
El cual se lee como El límite de f(x)f(x), cuando xx tiende a mm desde la dirección negativa, es igual a LL; lo cual significa que el valor de f(x)f(x) se acerca más y más a LL en lo que xx se acerca más y más a mm por el lado izquierdo. PERO recuerda, xx nunca llega a ser xx.

Límite por la derecha:  limx → m+f(x)=L\, lim_{x \, \to \, m^+} f(x) = L
El cual se lee como El límite de f(x)f(x), cuando xx tiende a mm desde la dirección positiva, es igual a LL; lo cual significa que el valor de f(x)f(x) se acerca más y más a LL en lo que xx se acerca más y más a mm por el lado derecho. PERO recuerda, xx nunca llega a ser mm.

Límite bilateral (límite ordinario): limx → mf(x)=L  \, lim_{x \, \to \, m} f(x) = L \, si y sólo si  limx → m+f(x)=L  \, lim_{x \, \to \, m^+} f(x) = L \, y  limx → m−f(x)=L  \, lim_{x \, \to \, m^-} f(x) = L \,