Área de curvas polares

Cuando queremos encontrar el área dentro de una sola ecuación polar utilizamos la siguiente fórmula:
$\large A=\int_{\alpha}^{\beta}\frac{1}{2}r^2d\theta$
Donde $\alpha$ es el ángulo inicial y $\beta$ el ángulo final.

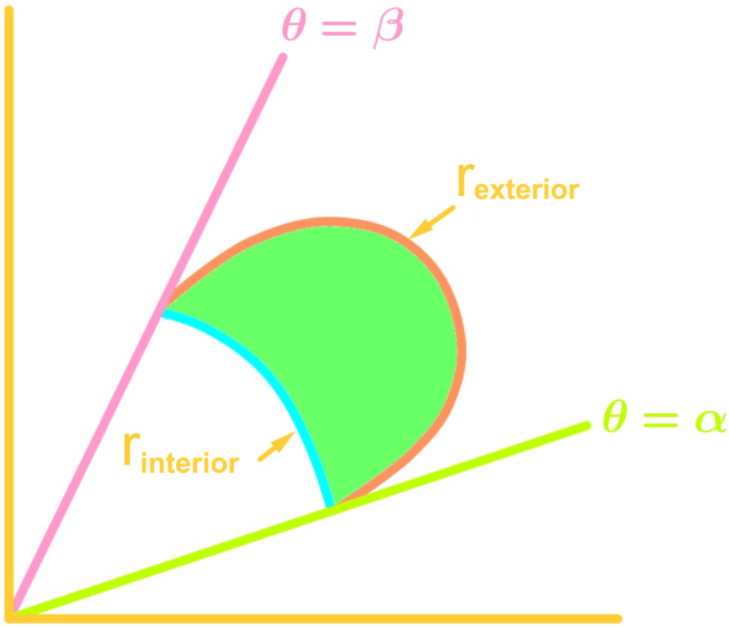
Para encontrar el área que se encuentra dentro de dos ecuaciones polares como se muestra en la imagen abajo, se usa la fórmula:

$\large A=\int_{\alpha}^{\beta}\frac{1}{2}(r^{2}\;_{exterior}-r^{2}\;_{interior})d\theta$
Donde $r_{exterior}$ representa la curva de la ecuación polar que se encuentra “más afuera” y $r_{interior}$ representa la curva de la ecuación polar que se encuentra “dentro”.