Notación de conjuntos por extensión

En esta lección aprenderemos a:

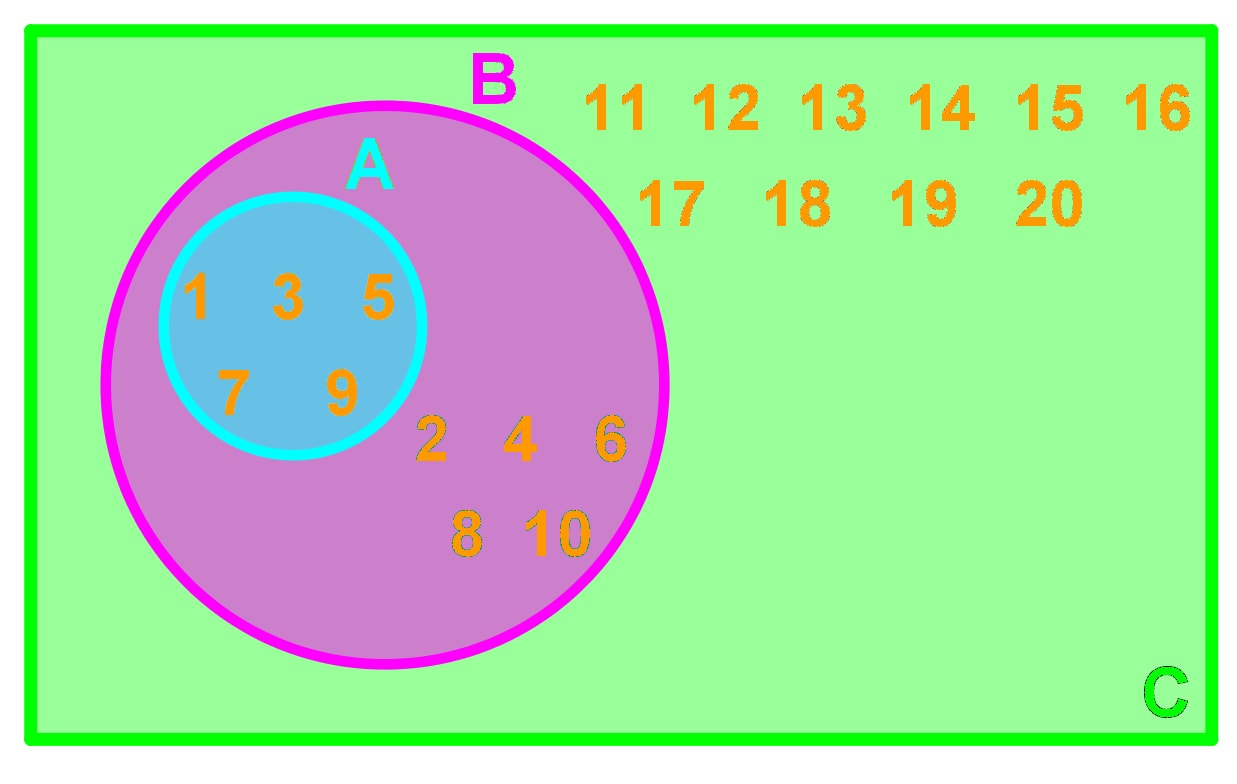
• Dibujar diagramas de Venn con conjuntos.
• Comprender qué es la notación de conjuntos.
• Dibujar e interpretar diagramas de Venn.

A continuación se presentan algunos términos que se usan en la notación de conjuntos:

• Conjunto: Un conjunto es una colección de elementos (usualmente números).
• Elemento: Objeto o número en un conjunto.
• $n(A)$: El número de elementos en $A$.
• Subconjunto: Un conjunto donde todos sus elementos pertenecen a otro conjunto.
• Conjunto universal: Conjunto de todos los elementos en un contexto particular.
• Conjunto vacío: Conjunto sin elementos.
• Conjunto unitario: Conjunto con sólo un elemento.
• Conjunto finito: Conjunto con una cantidad finita de elementos.
• Conjunto infinito: Conjunto con una cantidad infinita de elementos.
• Conjuntos disjuntos: Conjuntos que no tienen elementos en común.
• Complemento: Lista de elementos en un conjunto universal que quedan fuera de un conjunto seleccionado en particular. Si B es un conjunto, entonces el complemento se define como $B$ o $\overline B$.
• Conectores de disyunción inclusiva: El conector o se utiliza cuando los elementos del conjunto deben satisfacer alguna de las dos condiciones o ambas. En teoría de conjuntos esto también se representa con la unión ($\cup$).
• Conectores de conjunción: El conector y se utiliza cuando los elementos del conjunto satisface las dos condiciones simultáneamente. En teoría de conjuntos esto también se representa con la intersección ($\cap$).

Un conjunto es una lista de elementos a la cual se le nombra y sus elementos se listan usando corchetes {}. Un conjunto por extensión se escribe como:
$A$ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Donde:

• $A$ es el nombre del conjunto.
• El conjunto tiene 10 elementos, por lo tanto $n$ = 10.

La clave de escribir un conjunto por extensión es el tomar en cuenta a cada uno de los elementos en el conjunto y mencionarlo en la lista dentro de los corchetes.