En esta lección estudiaremos funciones matemáticas.
Cuando se tienen dos cantidades de distintos tipos, or en simple: dos variables, se dice que una es una función de la otra cuando su valor depende de la otra variable. En términos sencillos, una función es una relación de dependencia entre dos tipos de cantidades distintas; por ejemplo, en una gráfica de un plano cartesiano, una función se representa como la relación entre la variable x y la variable y, donde el valor de y depende del valor de entrada x.
Es importante mencionar, que no cualquier relación entre variables es igual a una función; en específico, una función definida por las variables x y y, tiene un valor único en y por cada valor de entrada x.
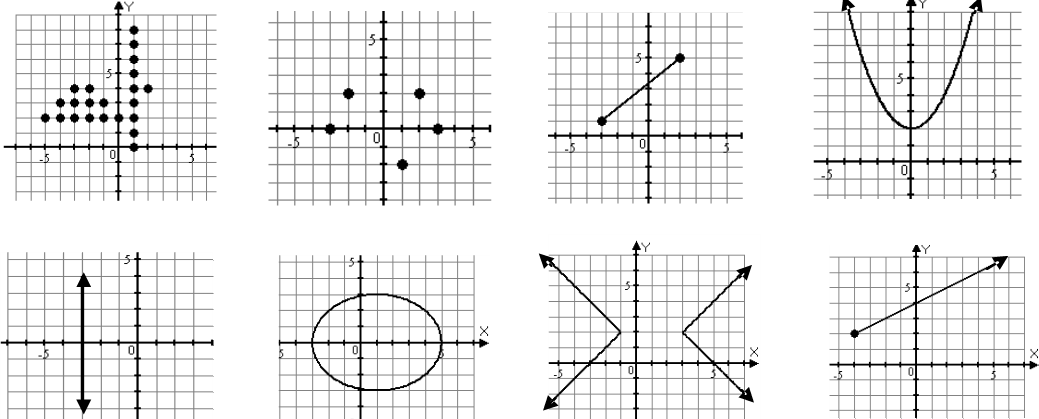
Una técnica muy sencilla para saber si una relación graficada en un plano cartesiano es una función es la prueba de la línea recta, y te la mostramos a continuación.