Sign In
Sign Up
flag-us

Mastering Single-Price Monopoly: Price & Output Decisions
Dive into the world of single-price monopoly! Understand how firms set prices, make output decisions, and impact consumer welfare. Perfect for economics students looking to excel in market structures.

  1. Intros0/3 watched
  2. Examples0/14 watched
  1. 0/3
  2. 0/14
Now Playing:Monopoly single price price and output decisions – Example 1a
Intros
0/3 watched
  1. Monopoly Single-Price: Price & Output Decisions Overview:
  2. Monopoly Single-Price: Price & Output Decisions Overview:
    Maximizing Profit with Total Revenue & Total Cost
    • Use a Table to Keep Track of Information
    • Calculate Total Revenue & Cost
    • Calculate Profit
    • Find the One with the Highest Profit
  3. Monopoly Single-Price: Price & Output Decisions Overview:
    Maximizing Profit with MR = MC
    • Graphically: Graph MR, MC, ATC and Demand
    • Find the intersection of MR and MC
    • Algebraically: Find equations and set MR = MC
    • Solve and find q and p
    • Find the Economic profit
Examples
0/14 watched
  1. Graphically Maximizing Profit
    Consider the following graph:

    Maximizing Profit
    1. Find the output and price which maximizes profit.

    2. Find the economic profit.

Monopoly definitions
Jump to:NotesConceptFAQsPrerequisites
Notes
The monopoly sets their output and price at a point in which it maximizes economic profit. There are two ways to do this:

Maximizing Profit with Total Revenue & Total Cost

Suppose we know the demand for the product, and the total cost of producing them. Then we can:
  1. Draw a table with the following columns: quantity, price, total revenue, total cost and profit.
  2. Calculate the total revenue ( p × q ).
  3. Calculate the profit (P = R - C ).
  4. Find the output with the highest attainable profit.

Price

(p)

Quantity demanded

(q)

Total Revenue

( R = p × q )

Total Cost

(C)

Profit

(P = R - C)

10

0

0

5

-5

9

1

9

7

2

8

2

16

10

6

7

3

21

14

7

6

4

24

19

5

5

5

25

25

0


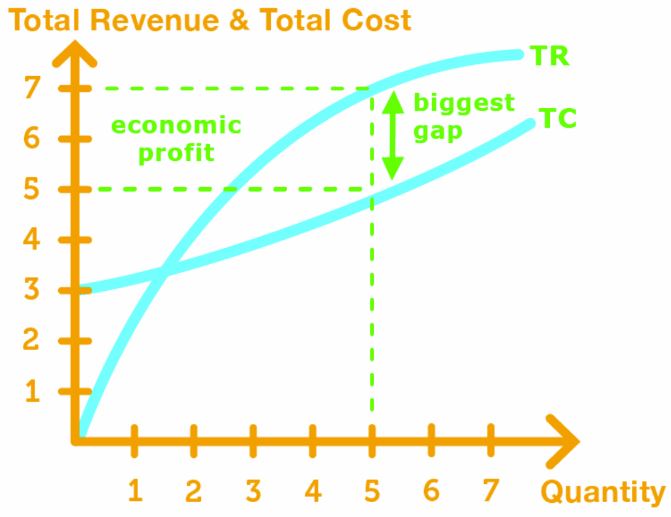
In this case, the highest attainable profit when the output produced is 3, the price is $7.

If we graph total revenue and total cost in a graph, then the highest attainable profit will be the output in which TR and TC have the biggest gap.

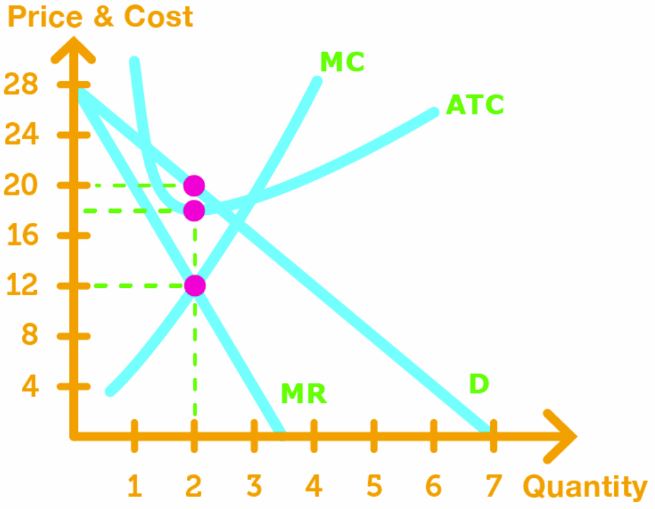
Monopoly: Maximizing profit with total revenue & total cost

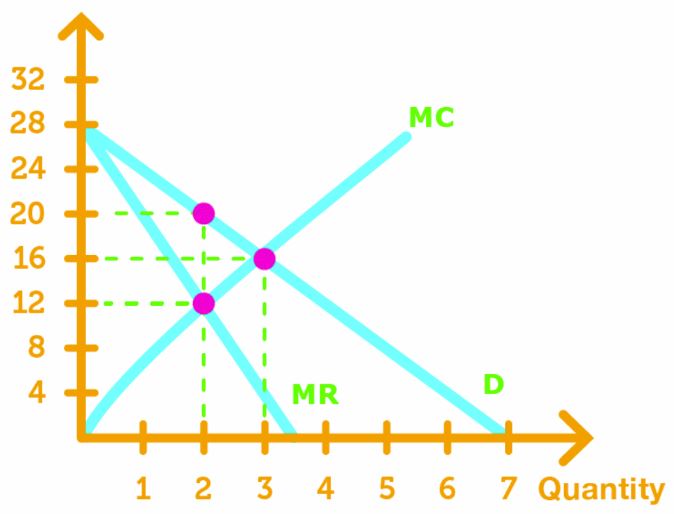
Maximizing Profit with MR = MC

Just like in perfect competition, monopolist find the output q and price p that maximizes profit by solving for MR = MC.

To solve p and q graphically, we do the following:
  1. Graph the MR, MC, ATC, and demand Curve
  2. Find the intersection point of MR and MC to find output q
  3. Use output q to find price p on the demand curve.

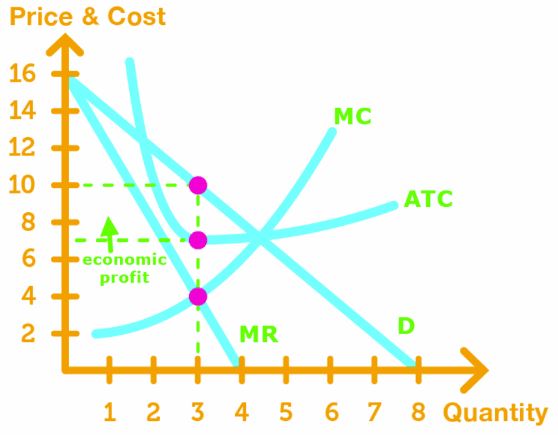
Monopoly: Maximizing profit with marginal revenue & marginal cost

To solve p and q graphically, we do the following:
  1. Define formulas for demand curve, MR and MC
  2. Set MR = MC and solve for output q
  3. Put output q into the demand formula and solve for p

To calculate economic profit, we find the average total cost ATC at the output q, and use the formula

Economic Profit = (p - ATC) q

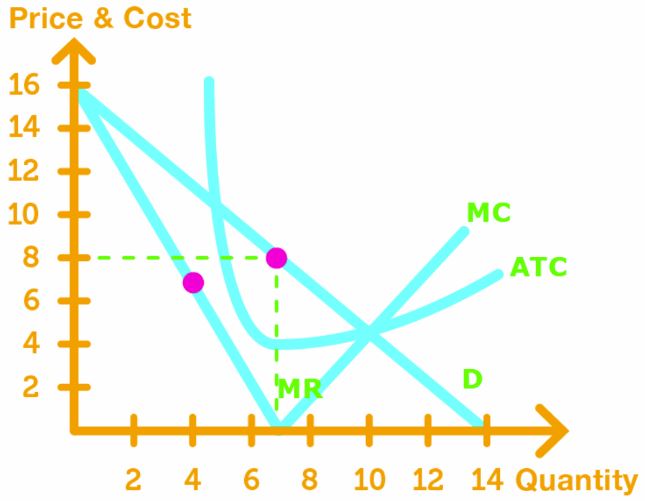
Deadweight Loss in Single-Price Monopoly

Unlike perfect competition, monopolist is inefficient because it creates deadweight loss.

Monopolist produces the output that maximizes profit, but there is a shortage because consumers want more of the product.

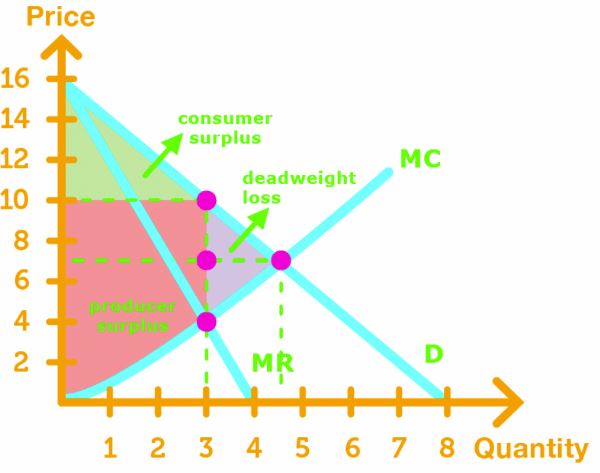
Deadweight Loss in single-price monopoly

Note 1: The deadweight loss and consumer surplus can be calculated by using the area of the triangle formula
A = bh2\large \frac{bh}{2}

Note 2: The producer surplus can be calculated by breaking apart the surplus into a triangle and square. Then calculate the areas of each to find the sum.
Concept

Introduction to Single-Price Monopoly

Welcome to our exploration of single-price monopoly, a fascinating concept in economics! This unique market structure occurs when a single firm dominates an industry and sets one price for all consumers. Our introduction video is a great starting point to grasp this concept. It visually explains how a single-price monopoly operates, making complex ideas more accessible. You'll learn about the firm's power to influence market prices and output levels, as well as the potential impacts on consumer welfare. The video also touches on real-world examples, helping you connect theory to practice. As we delve deeper into single-price monopoly, you'll discover its characteristics, advantages, and potential drawbacks. Remember, understanding this concept is crucial for grasping broader economic principles. So, let's dive in and unravel the intricacies of single-price monopoly together!

FAQs

Here are some frequently asked questions about single-price monopoly:

1. What is a single-price monopolist?

A single-price monopolist is a firm that has exclusive control over a market and charges the same price to all consumers. This type of monopoly doesn't engage in price discrimination, instead setting one uniform price for its product or service.

2. How does a single-price monopoly maximize profit?

A single-price monopoly maximizes profit by producing at the quantity where marginal revenue (MR) equals marginal cost (MC). It then charges the highest price consumers are willing to pay for that quantity, as determined by the demand curve.

3. What are the characteristics of a single-price monopoly?

Key characteristics include: sole seller in the market, no close substitutes for the product, high barriers to entry, price-setting power, and the ability to earn economic profits in the long run. However, they face a trade-off between price and quantity sold.

4. How is deadweight loss calculated in a single-price monopoly?

Deadweight loss in a monopoly is calculated by finding the area of the triangle formed between the monopoly price/quantity point, the competitive market equilibrium point, and the demand curve. This area represents the lost economic efficiency due to monopoly pricing.

5. What is the difference between a single-price monopoly and price discrimination?

A single-price monopoly charges all consumers the same price, while price discrimination involves charging different prices to different consumers or groups of consumers based on their willingness to pay. Price discrimination can potentially increase a monopoly's profits and reduce deadweight loss.

Prerequisites

Understanding the foundations of microeconomics is crucial when delving into complex topics like monopoly single-price pricing and output decisions. Two key prerequisite concepts that play a significant role in this area are consumer and producer surplus and deadweight loss.

When examining monopoly single-price strategies, a solid grasp of consumer and producer surplus is essential. This concept helps us understand the benefits that both consumers and producers derive from market transactions. In a monopoly situation, the distribution of these surpluses is significantly altered compared to a competitive market. The monopolist's ability to set prices affects the balance between consumer and producer surplus, often leading to a reduction in overall economic welfare.

Furthermore, the concept of deadweight loss becomes particularly relevant when analyzing monopoly pricing decisions. Deadweight loss represents the economic inefficiency that occurs when a market fails to achieve an optimal allocation of resources. In the context of a monopoly, the single-price strategy often results in a higher price and lower output compared to perfect competition, leading to a deadweight loss in the market.

By understanding consumer and producer surplus, students can better evaluate the impact of monopoly pricing on different market participants. This knowledge allows for a more comprehensive analysis of how a monopolist's decisions affect overall economic welfare and the distribution of benefits between consumers and the monopoly firm.

Similarly, familiarity with deadweight loss calculations provides insights into the efficiency costs associated with monopoly power. This understanding is crucial for assessing the societal impact of monopolies and forms the basis for discussions on potential regulatory interventions or policies aimed at mitigating the negative effects of monopolistic practices.

As students explore monopoly single-price strategies, they will find that these prerequisite topics serve as fundamental building blocks. The ability to analyze consumer and producer surplus in monopoly markets helps in understanding the motivations behind a monopolist's pricing decisions. Simultaneously, recognizing the deadweight loss associated with these decisions provides a critical perspective on the overall efficiency of monopoly markets.

In conclusion, a strong foundation in these prerequisite topics enhances students' capacity to engage with more advanced concepts in monopoly pricing and output decisions. It enables a more nuanced understanding of the economic implications of monopoly power and prepares students for deeper analyses of market structures and regulatory economics.