Sign In
Sign Up
flag-us

Mastering Parallel Line Proofs in Geometry
Dive into the world of parallel line proofs! Learn to identify key relationships, apply theorems, and construct airtight geometric arguments. Boost your problem-solving skills and excel in geometry.

  1. Intros0/1 watched
  2. Examples0/10 watched
  1. 0/1
  2. 0/10
Now Playing:Parallel line proofs– Example 0
Intros
0/1 watched
  1. Relationships between lines and angles
Examples
0/10 watched
  1. What is the value of x if AB‾\overline {AB} ∥\parallel CD‾\overline {CD} ?

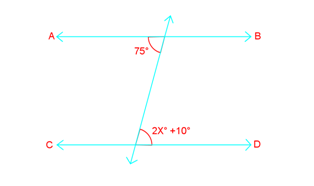
    1. Parallel line proofs: using alternate alternate interior angles theorem to find unknown


    2. Parallel line proofs: solving for x by corresponding angles theorem


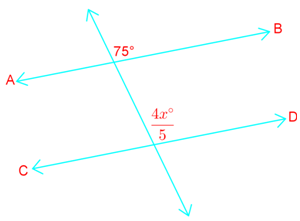
    3. Parallel line proofs: solve unknown by applying corresponding angles theorem

Parallel line proofs
Jump to:NotesConceptFAQsPrerequisites
Notes
Concept

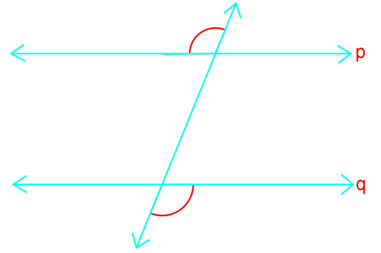
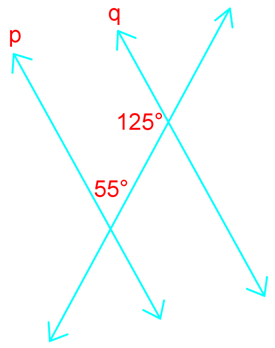
Introduction to Parallel Line Proofs

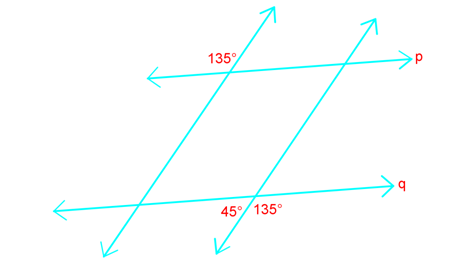
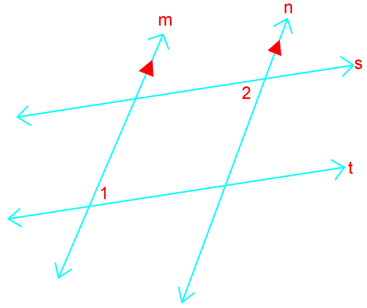
Welcome to the fascinating world of parallel line proofs! These proofs are essential in geometry, helping us understand the relationships between parallel lines and the angles they create. To kick off our journey, we'll start with an introduction video that lays the foundation for this concept. This video is crucial as it visually demonstrates how transversals and parallel lines interact, creating corresponding, alternate, and interior angles. As your math tutor, I'm excited to guide you through this topic. Parallel proofs may seem challenging at first, but with practice, you'll find them quite logical and even enjoyable. They're like solving parallel line puzzles, using what we know about parallel lines to prove other geometric relationships. Remember, mastering parallel line proofs will significantly boost your overall geometry skills. So, let's dive in and explore this fundamental concept together!

Understanding the transversals and parallel lines is key to mastering these proofs. By examining how parallel lines interaction with each other, we can deduce various properties and theorems. Additionally, recognizing the significance of interior angles formed by these lines will aid in solving complex problems. The more you practice, the more intuitive these concepts will become. So, let's continue to explore and enjoy the journey of learning parallel line proofs!

FAQs

Here are some frequently asked questions about parallel line proofs:

1. What are the 5 ways to prove that lines are parallel?

The five main ways to prove lines are parallel are: 1) Corresponding angles are congruent 2) Alternate interior angles are congruent 3) Alternate exterior angles are congruent 4) Same-side interior angles are supplementary 5) Two lines perpendicular to the same line are parallel

2. How do you prove that lines are parallel?

To prove lines are parallel, you need to show one of the following: - Corresponding angles are congruent - Alternate interior angles are congruent - Same-side interior angles are supplementary Use given information and geometric theorems to logically prove one of these conditions.

3. How do you prove equations are parallel?

To prove equations represent parallel lines: 1) Write equations in slope-intercept form (y = mx + b) 2) Compare the slopes (m values) 3) If slopes are equal, the lines are parallel Remember, parallel lines have the same slope but different y-intercepts.

4. How do you prove if two lines are parallel or not?

To prove if lines are parallel: 1) Check if corresponding or alternate interior angles are congruent 2) Verify if same-side interior angles are supplementary 3) Compare slopes if equations are given 4) Use the transitive property if both lines are parallel to a third line If any of these conditions are met, the lines are parallel.

5. What is the proof statement for parallel lines?

A typical proof statement for parallel lines is: "Given: (State given information about angles or lines) Prove: Line AB is parallel to Line CD" The proof then uses logical steps and geometric theorems to show that one of the conditions for parallel lines is satisfied.

Prerequisites

Understanding parallel line proofs is a crucial skill in geometry, but to master this concept, it's essential to have a solid foundation in several prerequisite topics. One of the most fundamental prerequisites is parallel lines and transversals. This topic introduces the key relationships between parallel lines and the angles formed when they are intersected by a transversal, which is the cornerstone of many parallel line proofs.

Another important prerequisite is the study of polygons. While it might not seem directly related, understanding polygons helps in visualizing and applying concepts like the alternate interior angles theorem, which is frequently used in parallel line proofs. This knowledge allows students to recognize and utilize angle relationships within more complex geometric figures.

Surprisingly, conics and circles also play a role in preparing for parallel line proofs. This topic introduces students to linear equations in the coordinate plane, which is crucial for understanding how parallel lines are represented algebraically and graphically. This algebraic perspective is often essential in more advanced parallel line proofs.

The concept of parallel and perpendicular lines in linear functions is directly relevant to parallel line proofs. This prerequisite topic provides the tools for proving lines are parallel using algebraic methods, complementing the geometric approaches and offering alternative proof strategies.

Lastly, while it might seem unrelated at first glance, combination of SohCahToa questions can be beneficial. This topic enhances students' ability in visualizing angle patterns, which is invaluable when working with complex parallel line configurations in proofs.

By mastering these prerequisite topics, students build a strong foundation for tackling parallel line proofs. Each topic contributes unique skills and perspectives: from understanding basic angle relationships and polygon properties to applying algebraic concepts and enhancing spatial visualization. This comprehensive background enables students to approach parallel line proofs with confidence, armed with a diverse set of tools and strategies.

Remember, geometry is a subject where concepts build upon each other. Skipping or glossing over these prerequisites can lead to difficulties in understanding and applying the principles of parallel line proofs. Therefore, it's crucial to invest time in thoroughly grasping these foundational topics. Doing so will not only make parallel line proofs more accessible but will also enhance overall geometric reasoning skills, setting students up for success in more advanced geometric concepts.