Sign In
Sign Up
flag-us

Mastering Central and Inscribed Angles in Circles
Dive into the world of circle geometry! Explore the fascinating relationships between central and inscribed angles, uncover key properties, and discover practical applications in mathematics and real life.

  1. Intros0/1 watched
  2. Examples0/5 watched
  1. 0/1
  2. 0/5
Now Playing:Central and inscribed angles in circles – Example 0b
Intros
0/1 watched
  1. What are Inscribed angles and Central angles?
Examples
0/5 watched
  1. Find x

    1. Using central angle to find inscribed angles in circles


    2. Using central angles and properties of isosceles triangles to find unknown angles in circles


    3. Central and inscribed angles in circles


    4. find unknown using the relationship between central angles

Tangent properties
Jump to:NotesConceptFAQsPrerequisites
Notes
Concept

Introduction

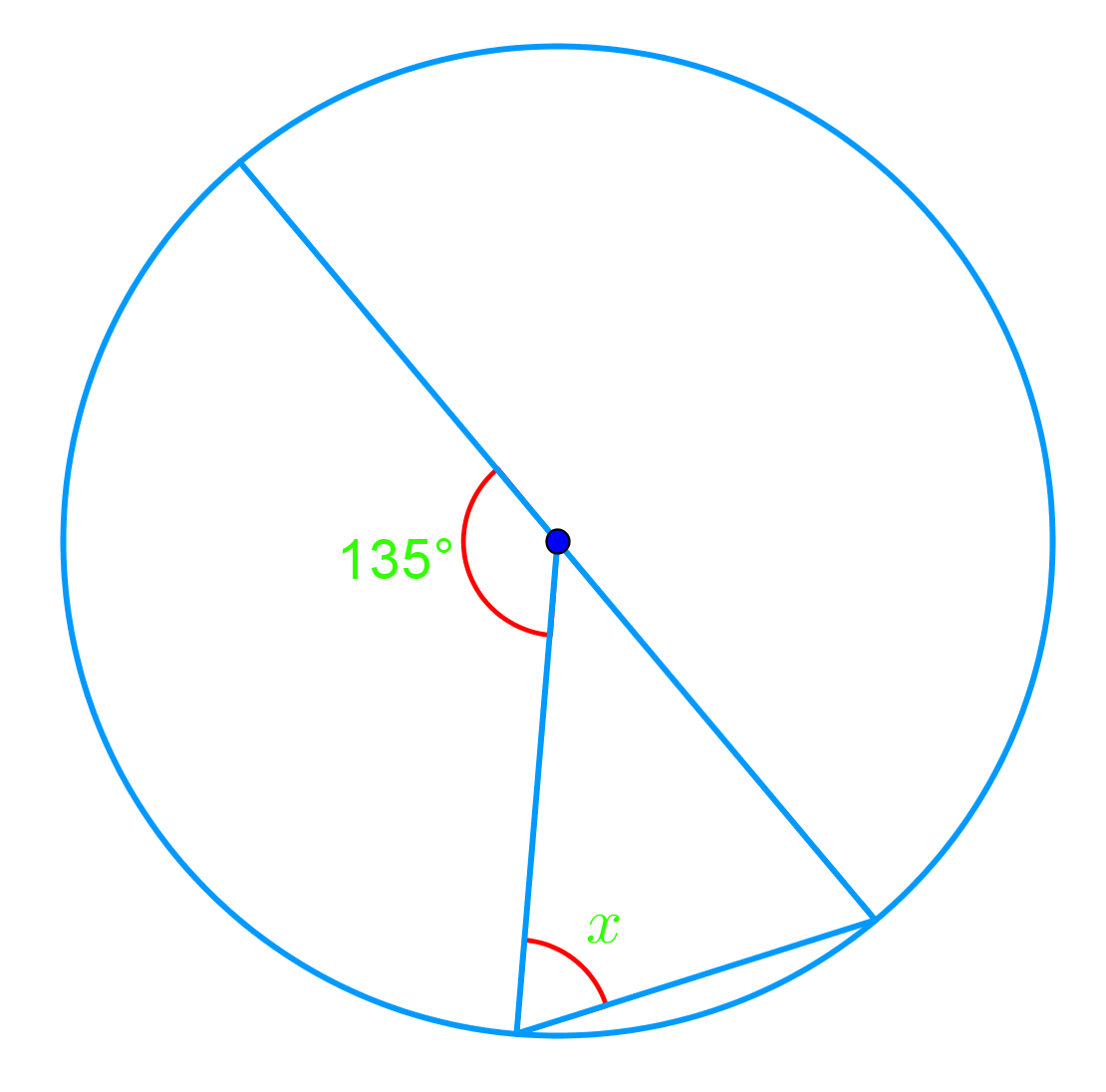
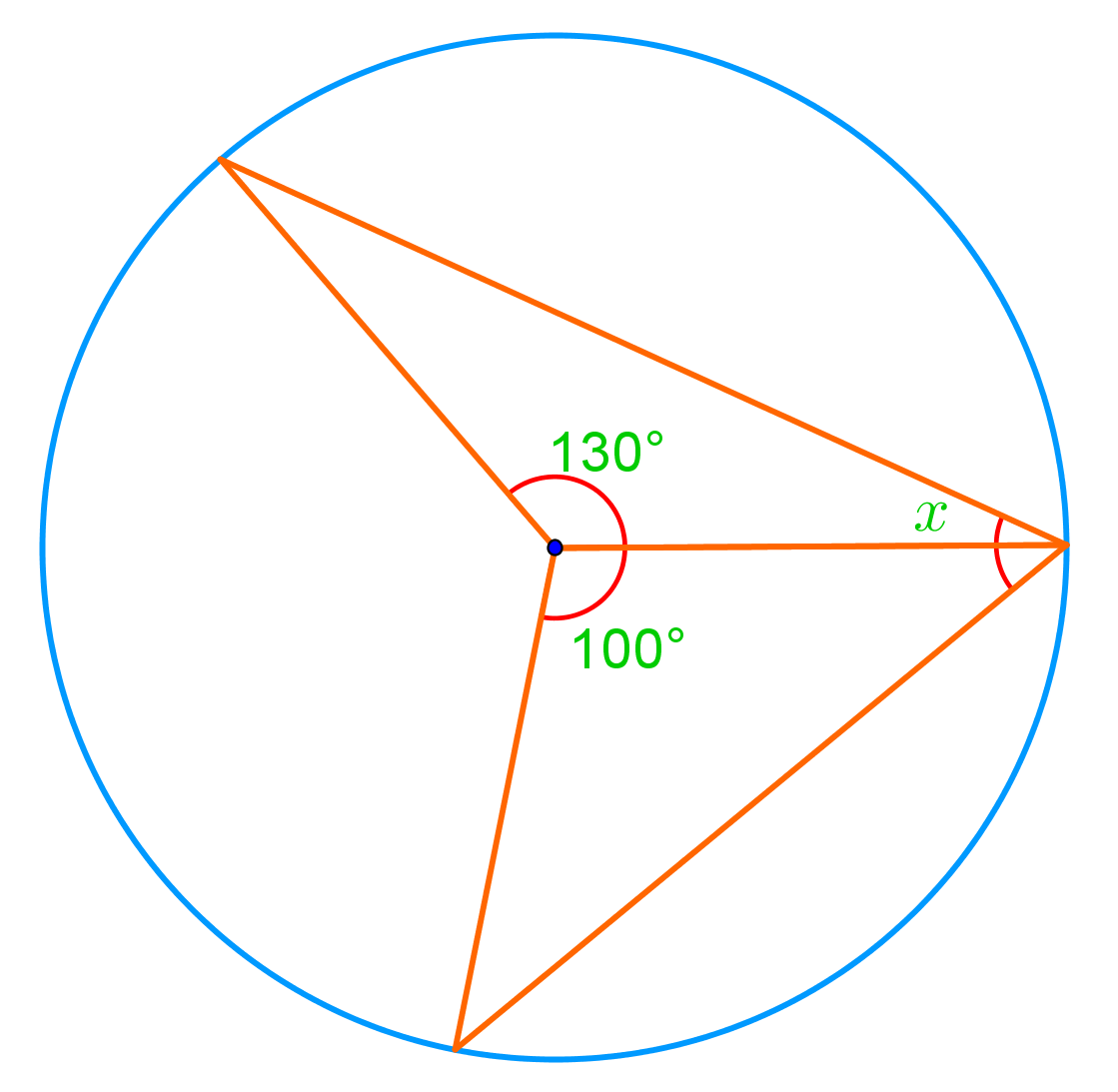
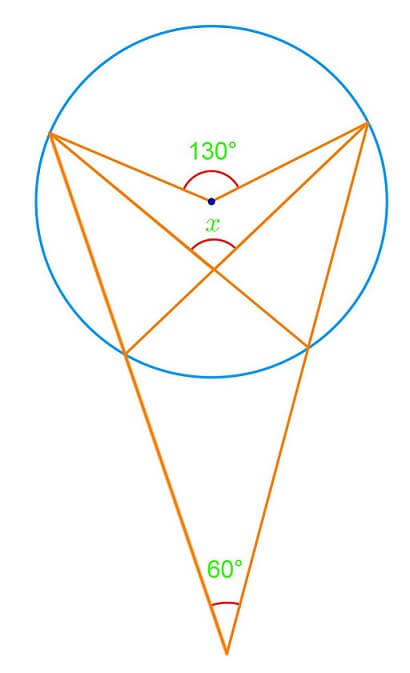
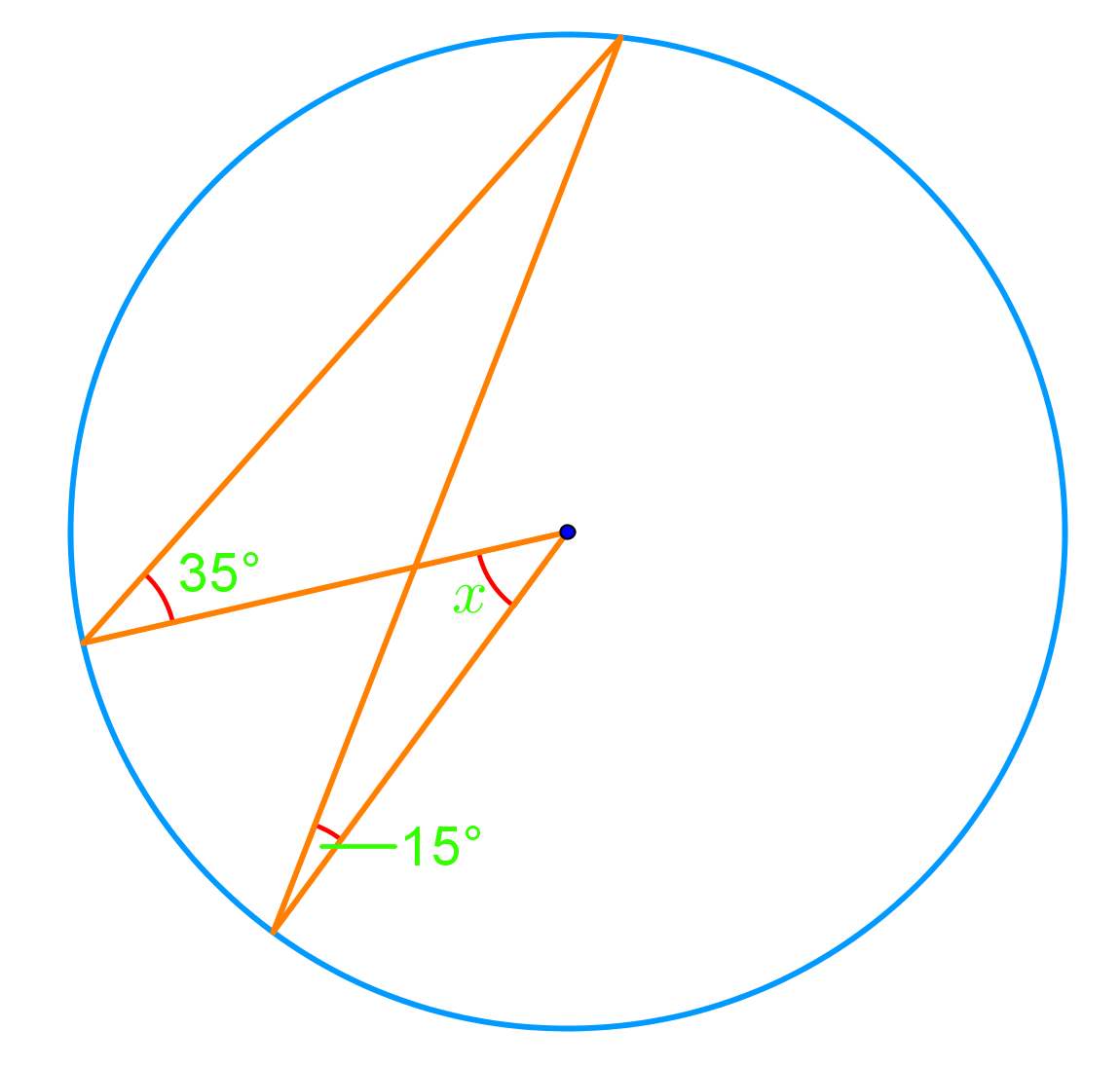
Circle geometry and inscribed angles are fundamental concepts in circle geometry, playing a crucial role in understanding the relationships between angles and arcs within circles. Our introduction video provides a comprehensive overview of these essential topics, serving as a valuable starting point for students and enthusiasts alike. This article delves into the key concepts, properties of inscribed angles, and relationships between angles and arcs, offering a deeper understanding of their significance in circular geometry. We'll explore how central angles, which have their vertex at the circle's center, differ from inscribed angles, which have their vertex on the circle's circumference. By examining these angles and their properties of inscribed angles, we'll uncover important theorems and practical applications in mathematics and real-world scenarios. Whether you're a student preparing for exams or simply curious about circle geometry, this exploration of central and inscribed angles will enhance your understanding of these fascinating mathematical concepts.

FAQs

Here are some frequently asked questions about central and inscribed angles:

1. How do you know if an angle is inscribed?

An angle is inscribed if its vertex lies on the circumference of a circle and its sides are chords of the circle. In other words, the angle is formed by two chords that intersect on the circle's edge.

2. Are central angles and inscribed angles measured the same way?

No, central angles and inscribed angles are not measured the same way. A central angle is measured directly as the angle formed at the center of the circle. An inscribed angle is measured as half the measure of the central angle that subtends the same arc.

3. What is the formula for inscribed angle?

The formula for an inscribed angle is: Inscribed Angle = (1/2) × Central Angle. This means that an inscribed angle is always half the measure of the central angle that subtends the same arc.

4. What is an example of a central angle?

A central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. For example, imagine a pizza cut into 8 equal slices. The angle formed at the center by any two adjacent slices is a central angle of 45° (360° ÷ 8).

5. How do you solve inscribed angles problems?

To solve inscribed angles problems: 1. Identify the inscribed angle and the arc it intercepts. 2. Remember that the inscribed angle is half the central angle subtending the same arc. 3. If given the central angle, divide by 2 to find the inscribed angle. 4. If given the inscribed angle, multiply by 2 to find the central angle. 5. Use the relationships between inscribed angles and arcs to solve for unknown angles or arc measures.

Prerequisites

Understanding central and inscribed angles in circles is a crucial concept in geometry, but to fully grasp this topic, it's essential to have a solid foundation in several prerequisite areas. One of the fundamental concepts to master is angles in a circle. This knowledge forms the basis for understanding how different types of angles relate to circular geometry.

Another important prerequisite is chord properties. Chords play a significant role in the study of central and inscribed angles, as they often form the basis for these angles within a circle. Understanding how chords behave and their relationships to angles is crucial for solving problems involving central and inscribed angles.

To delve deeper into the topic, familiarity with inscribed angles and proofs is essential. This knowledge helps in understanding the relationships between inscribed angles and the arcs they intercept, which is a key aspect of the main topic.

Additionally, knowledge of isosceles and equilateral triangles can be beneficial, as these shapes often appear when working with central and inscribed angles in circles. The properties of these special triangles can simplify many calculations and proofs related to circular geometry.

For a more advanced understanding, radian measure and arc length concepts are valuable. These topics provide alternative ways to measure angles and arcs in circles, which can be particularly useful in more complex problems involving central and inscribed angles.

When dealing with calculations, the ability to use tangent ratio to calculate angles and sides can be incredibly helpful. This trigonometric skill often comes into play when solving problems related to central and inscribed angles, especially when dealing with right triangles inscribed in circles.

For those looking to explore more advanced applications, understanding double-angle identities can be beneficial. These trigonometric identities sometimes appear in complex problems involving central and inscribed angles, particularly when dealing with angles that are twice the measure of others.

Lastly, recognizing the relationship between two variables is a valuable skill that applies to many aspects of mathematics, including the study of central and inscribed angles. This algebraic concept helps in understanding how changes in one angle or measurement affect others within a circle.

By mastering these prerequisite topics, students will be well-equipped to tackle the complexities of central and inscribed angles in circles, enabling them to solve a wide range of geometric problems with confidence and precision.