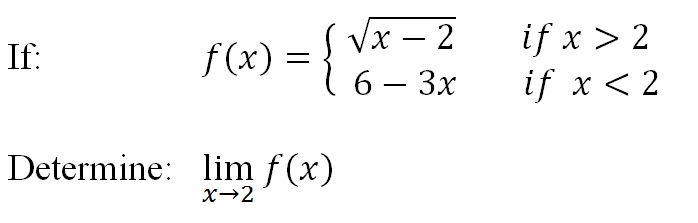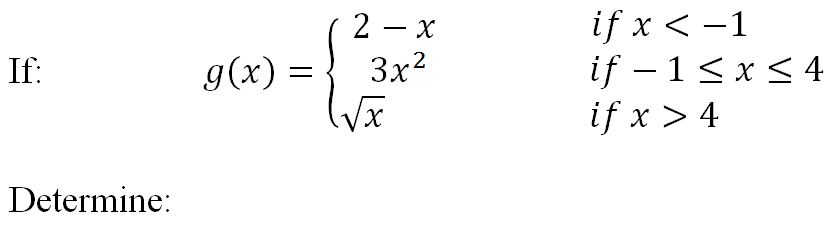Sign In
Sign Up
flag-us

Mastering Direct Substitution for Algebraic Limit Evaluation
Unlock the power of direct substitution in calculus. Learn when and how to apply this technique for efficient limit evaluation, and boost your problem-solving skills in advanced mathematics.

Get the most by viewing this topic in your current grade. Pick your course now.

Now Playing:Finding limits algebraically by direct substitution – Example 0a
Intros
  1. No more finding limits "graphically"; Now, finding limits "algebraically"!
    What is Direct Substitution?
Examples
  1. Evaluate the limit:
    1. lim⁡x→3(5x2−20x+17)\lim_{x \to 3} (5x^2-20x+17)

    2. lim⁡x→−2x3+3x2−15−4x\lim_{x \to -2} \frac{{{x^3} + 3{x^2} - 1}}{{5 - 4x}}

    3. lim⁡x→0∣x∣\lim_{x \to 0}\left| x \right|

    4. lim⁡x→π2  sin⁡x2−cos⁡x\lim_{x \to \frac{\pi }{2}} \;\frac{{\sin x}}{{2 - \cos x}}

Introduction to Calculus - Limits
Jump to:NotesConceptFAQsPrerequisites
Notes
Graphically finding the limit of a function is not always easy, as an alternative, we now shift our focus to finding the limit of a function algebraically. In this section, we will learn how to apply direct substitution to evaluate the limit of a function.
• if: a function ff is continuous at a number aa
then: direct substitution can be applied: lim⁡x→a−f(x)=lim⁡x→a+f(x)=lim⁡x→af(x)=f(a)\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) =\lim_{x \to a} f(x)= f(a)

• Polynomial functions are continuous everywhere, therefore "direct substitution" can ALWAYS be applied to evaluate limits at any number.
Concept

Introduction: Finding Limits Algebraically with Direct Substitution

In the realm of calculus, finding limits is a fundamental concept in calculus that has evolved from graphical to more precise algebraic methods. This shift has revolutionized how we approach limit problems, offering a more systematic and accurate approach. At the forefront of these algebraic techniques is direct substitution, a powerful tool that simplifies the process of evaluating limits. Direct substitution allows us to find limits by simply plugging in the value that the variable is approaching, making it an essential skill for any calculus student. Our introduction video serves as a crucial starting point, providing a clear and concise overview of this topic. It lays the groundwork for understanding how direct substitution works and why it's so important in calculus. By mastering this technique, students can tackle a wide range of limit problems with confidence, setting the stage for more advanced concepts in calculus.

FAQs

Q1: What is the direct substitution method used for?
A1: The direct substitution method is primarily used for evaluating limits of functions. It involves replacing the variable in a function with the value that it's approaching to find the limit. This method is most effective for continuous functions where the limit exists and equals the function's value at that point.

Q2: What is the meaning of direct substitution property?
A2: The direct substitution property states that for a function f(x) that is continuous at a point a, the limit of f(x) as x approaches a is equal to f(a). In other words, you can directly substitute the value a into the function to find the limit, provided the function is continuous at that point.

Q3: How to use direct substitution to evaluate the limit?
A3: To use direct substitution, follow these steps: 1. Identify the value that x is approaching (let's call it 'a'). 2. Replace all instances of x in the function with 'a'. 3. Simplify and evaluate the resulting expression. If this process yields a defined value, that value is the limit.

Q4: When does direct substitution fail?
A4: Direct substitution can fail in several scenarios: 1. When the function is undefined at the point of interest. 2. For rational functions where substitution leads to division by zero. 3. When dealing with removable discontinuities. 4. For piecewise functions at the boundary points between pieces. In these cases, alternative methods like algebraic manipulation or one-sided limits may be necessary.

Q5: What are the advantages of using direct substitution?
A5: Direct substitution offers several advantages: 1. Simplicity and speed in solving limit problems. 2. It's intuitive and easy to understand for beginners. 3. It works well for a wide range of continuous functions. 4. It can quickly verify results obtained through other methods. 5. It's particularly useful in applications where function values at specific points are needed.

Prerequisites

Understanding the prerequisite topics is crucial when delving into the concept of "Finding limits algebraically - direct substitution." These foundational concepts provide the necessary groundwork for mastering this important calculus technique. Let's explore how these prerequisites relate to our main topic and why they're essential for your mathematical journey.

To begin with, a solid grasp of continuous functions is vital. Continuous functions form the basis for understanding limits, as they behave predictably as we approach specific points. This knowledge directly applies to direct substitution, where we can often simply plug in the limit point to find the function's value.

Similarly, familiarity with piecewise functions is important. These functions can present unique challenges when finding limits, as the behavior near the limit point may differ depending on which piece of the function we're considering. Understanding how to evaluate piecewise functions prepares you for more complex limit scenarios.

A strong foundation in polynomial functions is also crucial. Many limit problems involve polynomials, and knowing how to manipulate and simplify these expressions is key to successful direct substitution. Additionally, knowledge of rational functions is beneficial, as limits of rational functions often require special techniques when direct substitution leads to indeterminate forms.

Understanding absolute value functions and trigonometric functions broadens your ability to tackle a wide range of limit problems. These function types often appear in calculus and require careful consideration when applying direct substitution techniques.

Familiarity with radical functions is another important prerequisite. Radicals can complicate limit calculations, and knowing how to simplify and manipulate them is essential for successful direct substitution.

It's also beneficial to understand the broader context of evaluating limits algebraically, including cases where direct substitution isn't possible. This knowledge helps you recognize when direct substitution is applicable and when other techniques are needed.

Lastly, proficiency in factoring to find limits is invaluable. Techniques like finding the difference of squares can be crucial in simplifying expressions before applying direct substitution, often turning seemingly complex limits into straightforward calculations.

By mastering these prerequisite topics, you'll be well-equipped to tackle the challenges of finding limits algebraically through direct substitution. Each concept builds upon the others, creating a strong foundation for your calculus studies and beyond.