Continuity - Limits

Notes:

• Definition of “continuity” in everyday language
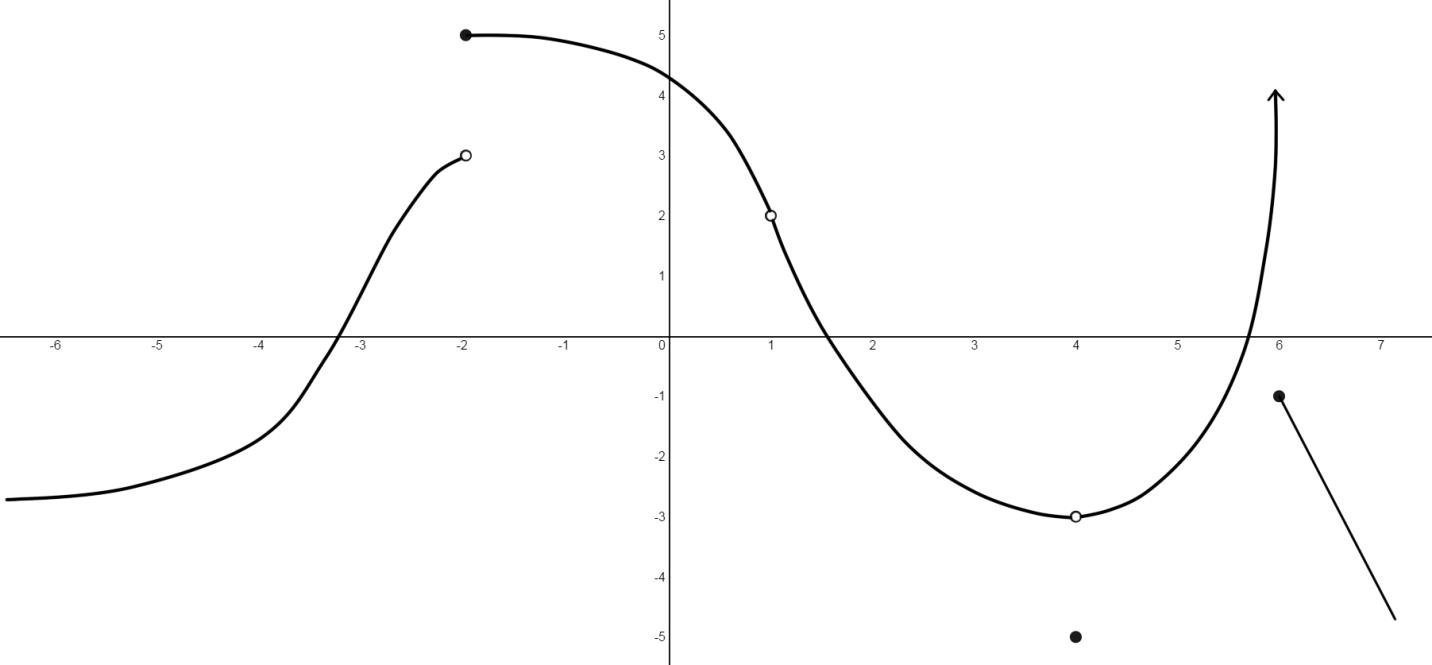
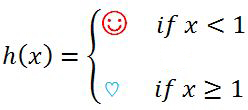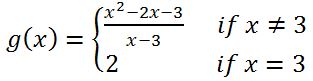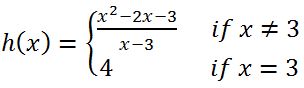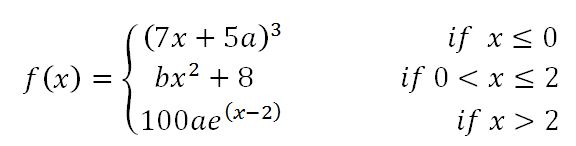A function is continuous if it has no holes, asymptotes, or breaks. A continuous graph can be drawn without removing your pen from the paper.

• Definition of “continuity” in Calculus
A function $f$ is continuous at a number a, if: $\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = f(a)$

• Polynomials are always continuous everywhere. Rational functions are continuous wherever the functions are defined; in other words, avoiding holes and asymptotes, rational functions are continuous everywhere. A function f is continuous at a number a, if and only if:
$\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = f(a)$

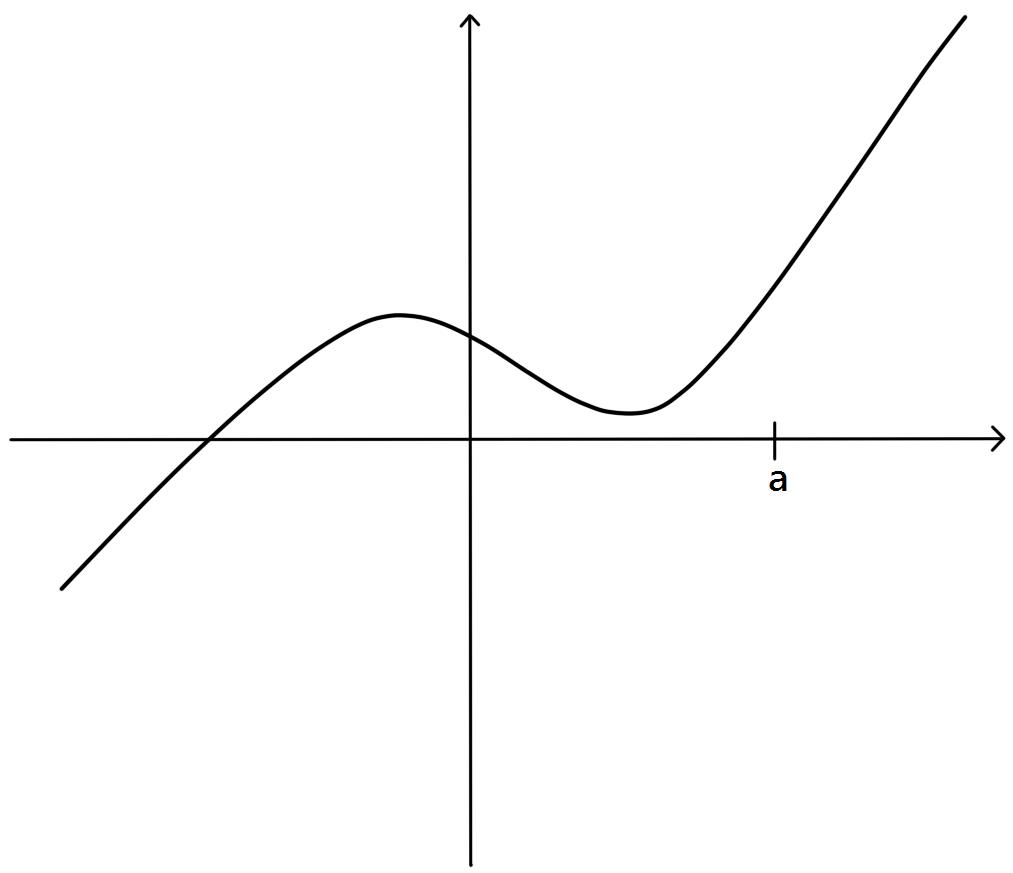
In simple words, the graph of a continuous function has no break in it and can be drawn without lifting your pen from the paper.