Waves Behaving Like Particles: Unraveling Quantum Mysteries

Dive into the fascinating world of quantum mechanics and explore how waves can exhibit particle-like properties. Understand key experiments and their implications in modern physics and technology.

In this lesson, we will learn:

• Waves behave like particle
• Property of the spectrum emitted from the hot bodies
• Photoelectric effect
• Compton effect

• Hot bodies contain vibrating particles, which radiate electromagnetic waves.
• Looking through a prism at light coming from an incandescent lamp, you will see colors of rainbow.

• The bulb also emits infrared radiation that you cannot see.
• The spectrum of incandescent bodies shows different color at different temperatures and various frequencies.
• Energy is emitted at variety of frequencies that depend on the temperature.
• As temperature increases the frequency increases.
• To explain the shape of the spectrum, Plank assumed that energy is not continues. He assumed that the energy of vibration of the atoms in a solid have only specific frequencies,

$E = nhf$
$f$: Frequency
$h$: Plank’s constant
$n$: Integer such as (0,1,2,3, 4. . . )

• This behavior is described by saying that energy is “quantized”, package of specific amounts.
• He also proposed that atoms do not always radiate electromagnetic waves as they vibrate, the radiation is emitted only when their vibrating energy changes. For instance, if the energy of an atom changes from $4h f$ to $3h f$, atom emits radiation.

• Energy comes in little bundles, quanta (plural of quantum), quanta is the smallest bundle of energy, we can not have an amount of energy smaller than quanta, like we can not have an amount of charge smaller than one electron.
• As you move up the stairs, they are certain levels at which you can stand, you cannot stand between the steps,
• In similar ways electrons around an atom exist at different energy levels, electrons jump around randomly from one layer to another, we cannot say exactly where they are, but we can say where they are likely to be Circles representing different levels of energy associated with electrons

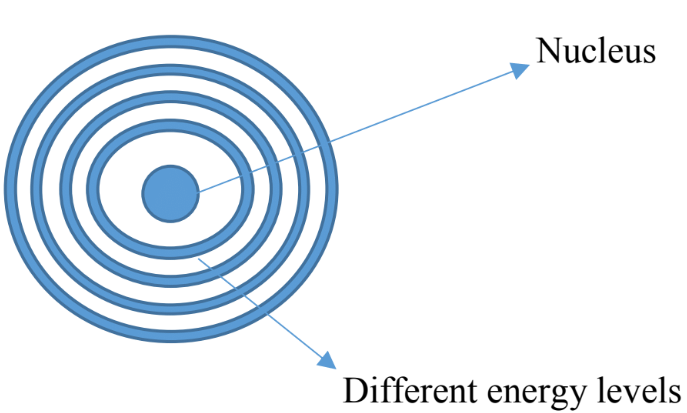
• The further we move from the nucleus the higher the amount of energy
• According to the quantum mechanics theory, electrons can exist one energy level or another but not anything between, so the energy is quantized, we can have only discrete amount of energy.
• So the Planck’s hypothesis states that molecular oscillations are quantized; their energy E can only be integer ($n$) multiplies of $hf$, where h is the Planck’s constant and $f$ is the natural frequency of oscillations:

• A negatively charged zinc plate discharges when ultra violet radiation falls on it, but it remains charged when ordinary visible light falls on it.
• The positively charged zinc plate does not charge similarly.
• Further study showed that the negatively charged zinc plate was discharged by losing or emitting electrons.
• The emission of electron upon upon electromagnetic radiation is called the “photoelectric effect”.

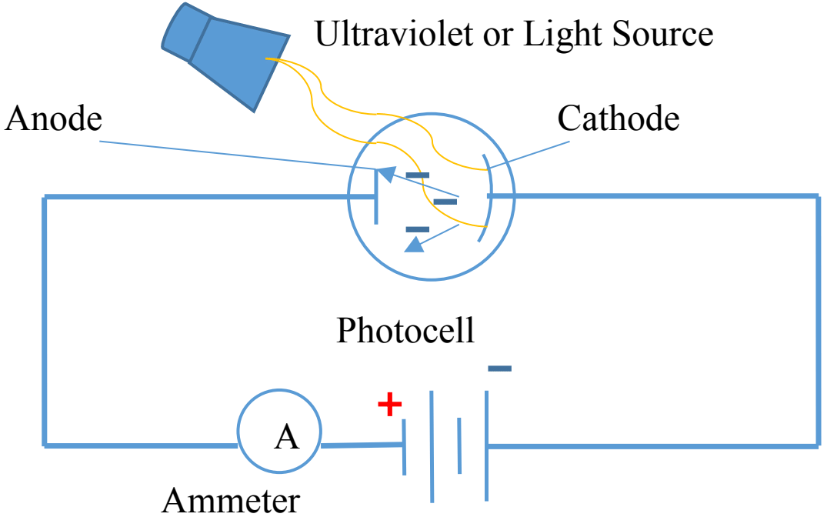
• Photoelectric cell contains two metal electrodes sealed in evacuated tube.
• The larger electrode, cathode, is coated with cesium.
• The second electrode, anode, made of a thin wire to block only smallest amount of radiation.
• The potential difference across the electrodes attract the electrons.
• Only specific type of radiation produces current in the circuit which is read by the ammeter.
• The frequency that produces current in the circuit called “threshold frequency”, $f_{0}$
• Frequency below $f_{0}$, does not eject any electrons, no matter how intense the light is.
• Frequency above $f_{0}$, ejects electrons , even if the light is very dim.
• According to wave model, intensive light should knock more electrons but, in this case is not true.
• So the photoelectric effect can not be explained by wave model of light.
• The only way to explain this phenomenon is the particle model of light.
• According to Einstein, light and other forms of radiation consist of discrete bundles of energy, called “photons”.
• Energy of each photon depends on the frequency of the light.

• The photoelectric effect reveals that a photon, even though it has no mass, has kinetic energy. So according Einstein, photon has another particle property, momentum.


• Since photon is travelling as fast as light, we cannot use the $p = mv$ equation to find the photon’s momentum.


• For those particles that travel at speed of light, momentum is calculated using special relativity, which allows massless particles to have momentum.


• Momentum of a photon is: $p= h/\lambda$, where h is the Plank’s constant.
  $h =$6.626 x 10^-34J.s $\qquad \lambda =$ wavelength in meters.


• The energy of photon is calculated using; $E = hf \enspace \Rightarrow \enspace E = \frac{hc} {\lambda}$
  
  and $\lambda = c.T = c/f \, \Rightarrow \, f = c/\lambda$


• To study the nature of photons, Compton directed X-rays of known wavelength at a graphite retarget, the wavelength of the scattered X-ray was longer than the original one.


• The above equation shows that the energy of a photon is inversely proportional to its wavelength. The increase in wavelength observed by Compton, means that the X-ray photons had lost both energy and momentum.

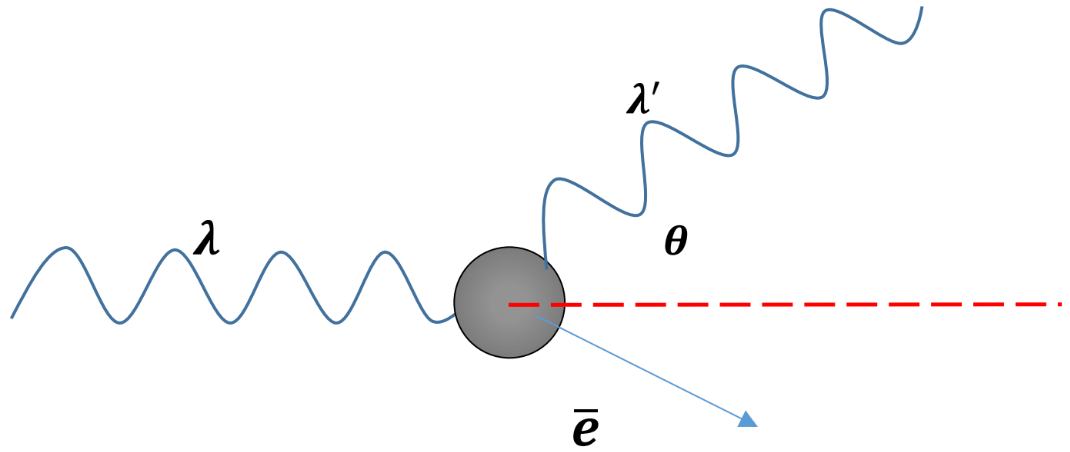
• The shift in the energy of scattered photons is called “Compton effect”.
• Compton observed that electrons were ejected from the graphite block, so the energy and momentum of the photons are transferred to electrons, similar to the elastic collisions of particles.
• Therefore, a photon is a particle that has energy and momentum.