Sign In
Sign Up
flag-ca

Mastering Vibration and Energy in Physics
Dive into the fascinating world of vibration and energy. Understand oscillations, various forms of energy, and their interconnections. Perfect for students seeking to grasp fundamental physics concepts and their practical applications.

  1. Intros0/3 watched
  2. Examples0/12 watched
  1. 0/3
  2. 0/12
Now Playing:Vibration and energy1 – Example 0a
Intros
0/3 watched
  1. Vibration
  2. Hooke's Law
Examples
0/12 watched
  1. When a family of three with a total mass of 150kg steps into their 1100kg car, the car's spring compresses 2.0cm.
    1. What is the spring constant of the car's spring?

    2. How far will the car lower if loaded with 400kg?

Vibration and energy
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • Vibrating and oscillating systems
  • Hooke’s law
  • How to find the amount of energy stored in a vibrating system?

Notes:

  • There are many examples of vibrating objects around us, an object attached to the end of spring, guitar strings, ruler held firmly at the end of the table.
  • During vibration (oscillation) the object moves back and forth about a fixed position called “equilibrium position”.
  • Let’s consider a mass vibrating at the end of a uniform spring.;
\qquad \quad (a) The mass is at its equilibrium position, there is no force exerted.

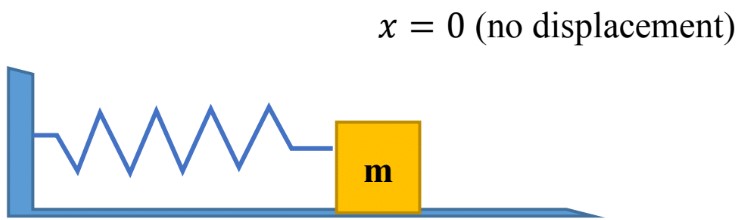
Vibration and energy


\qquad \quad (b) The mass is oscillating; the restoring force tries to pull the mass back to its equilibrium position.
Vibration and energy


\qquad \quad (c) The mass is oscillating; the restoring force tries to push the mass back to its equilibrium position.
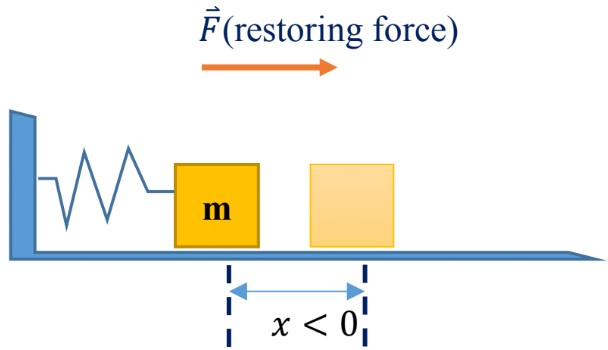
Vibration and energy


Hooke’s Law
  • The magnitude of the restoring force is directly proportional to the displacement xx;
    F∝xF \propto x
  • The direction of the restoring force is always opposite to the displacement which is indicated by a minus sign in the equation.

    F=−kxF = - kx (Hooke’s Law)


FF: Force exerted by the spring on the mass
KK: Spring constant
xx: Displacement

Energy
  • As we know the mechanical energy of a system is the sum of kinetic and potential energies.
  • In the case of the spring-mass system, the potential energy would be in the form of elastic potential energy in the spring which is calculated using the following equation;

PE=12kx2 PE = \frac{1}{2}kx^{2}


Therefore; the mechanical energy of the system is;

E=12mv2 + 12kx2E = \frac{1}{2}mv^{2} \, + \, \frac{1}{2}kx^{2}

\qquad \quad (a) At the extreme points where the mass stops momentarily to change the direction; vv = 0, xx = AA (amplitude, maximum displacement)

E=12kA2 E = \frac{1}{2}kA^{2} \, (1)

\qquad \quad (b) At the equilibrium position the mass moves with maximum velocity;

V=Vmax,x=0V = V_{max},x = 0


E=12mvmax2E = \frac{1}{2} mv^{2} _{max} (2)


From (1) and (2);

12kA2=12mvmax2⇒Vmax2=(km) A2 \frac{1}{2}kA^{2} = \frac{1} {2}mv^{2} _{max} \quad \Rightarrow \quad V^{2} _{max} = (\frac{k}{m}) \, A^{2}


\qquad \quad (c) At intermediate points, the energy is a part kinetic and part potential;

12mv2 + 12kx2=12kA2 \frac{1}{2}mv^{2} \, + \, \frac{1}{2}kx^{2} = \frac{1}{2}kA^{2}
    \qquad
  • From the above equation we can find velocity as the function of position;

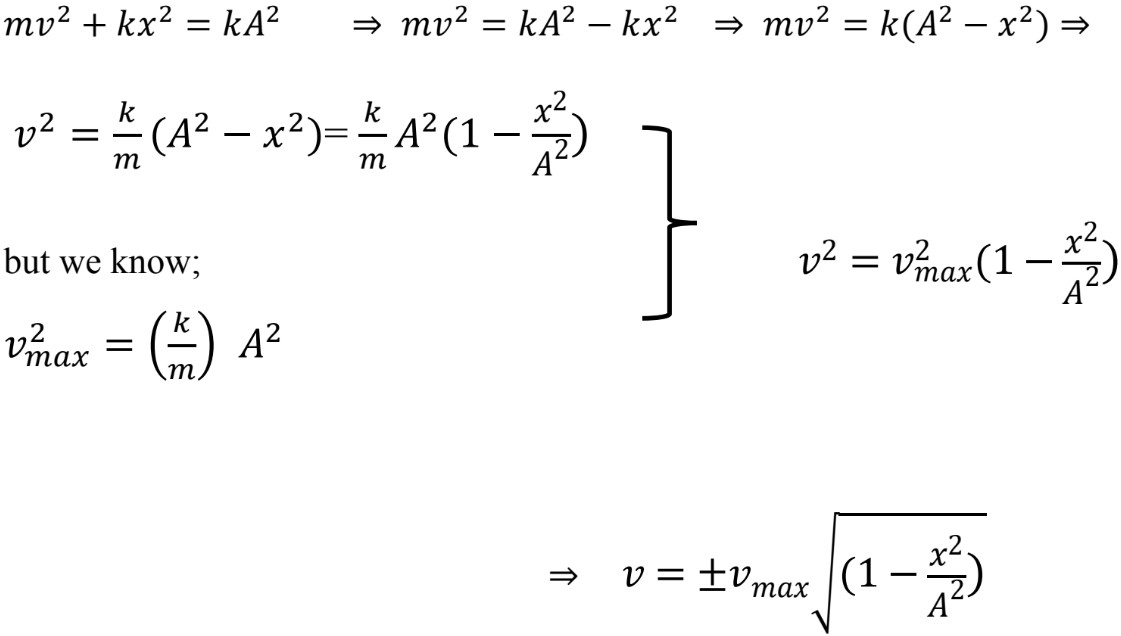
Vibration and energy


This gives the velocity of the object at any position.
Concept

Introduction to Vibration and Energy

Welcome to our exploration of vibration and energy in physics! These fundamental concepts are crucial for understanding how the world around us works. Vibration, also known as oscillation, is a repetitive motion around an equilibrium point. It's everywhere - from the strings of a guitar to the atoms in a crystal. Energy, on the other hand, is the capacity to do work and comes in various forms like kinetic energy, potential energy, and thermal. The interplay between vibration and energy is fascinating, as one often transforms into the other. Our introduction video will dive deeper into these concepts, providing visual examples and clear explanations. It's an essential starting point for grasping these ideas, which form the foundation for more advanced topics in physics. As we progress, you'll see how vibration and energy are interconnected and how they apply to real-world phenomena. So, let's get ready to explore these exciting concepts together!

FAQs

  1. What is the difference between vibration and oscillation?

    Vibration and oscillation are closely related concepts, often used interchangeably. Vibration typically refers to mechanical oscillations, usually of a higher frequency, while oscillation is a more general term that can apply to any repetitive variation around an equilibrium point. In physics, both describe a back-and-forth motion, but vibration is often associated with more rapid movements in solid objects.

  2. How does Hooke's Law relate to vibrating systems?

    Hooke's Law is fundamental to understanding many vibrating systems, especially those involving springs. It states that the force (F) needed to extend or compress a spring is directly proportional to the distance (x) of displacement from its equilibrium position, expressed as F = -kx, where k is the spring constant. This law explains why many vibrating systems exhibit simple harmonic motion and helps in calculating the frequency and period of oscillations.

  3. What is the relationship between energy and amplitude in an oscillating system?

    In an oscillating system, the total energy is directly related to the square of the amplitude. The formula for total energy in a simple harmonic oscillator is E = ½kA², where k is the spring constant and A is the amplitude. This means that doubling the amplitude quadruples the energy in the system. The energy constantly shifts between kinetic and potential forms throughout the oscillation, but the total energy remains constant in an ideal system.

  4. How does damping affect an oscillating system?

    Damping reduces the amplitude of oscillations over time by dissipating energy from the system. In a damped system, the oscillations gradually decrease in amplitude and eventually stop. The degree of damping affects how quickly this happens. Underdamped systems oscillate with decreasing amplitude, critically damped systems return to equilibrium fastest without oscillating, and overdamped systems return to equilibrium without oscillating but more slowly than critically damped systems.

  5. Can you explain the concept of resonance in vibrating systems?

    Resonance occurs when an oscillating system is driven at its natural frequency, causing it to oscillate with increased amplitude. This happens when the driving frequency matches the system's natural frequency, allowing for efficient energy transfer. Resonance can lead to dramatically increased amplitudes of vibration, which can be both useful (as in musical instruments) and potentially destructive (as in bridges subjected to wind or earthquake forces). Understanding resonance is crucial in engineering and physics for designing stable structures and efficient energy transfer systems.

Prerequisites

To fully grasp the concept of vibration and energy, it's crucial to have a solid foundation in several key areas of physics. One of the most fundamental prerequisites is understanding simple harmonic motion, which forms the basis for many vibrational systems. This concept helps explain how objects oscillate around an equilibrium position, a principle that's essential in studying various forms of vibration.

Another critical aspect of vibration and energy is the relationship between motion and energy. This is where knowledge of rotational kinetic energy and angular momentum becomes invaluable. Understanding how energy is stored in rotating objects and how it relates to their angular momentum provides insights into more complex vibrational systems, especially those involving circular or rotational motion.

When delving deeper into energy concepts related to vibration, it's essential to grasp the principles of electric potential and electric potential energy. This knowledge is particularly relevant when studying vibrations in electrical systems or when considering the energy stored in oscillating charged particles. The potential energy formula learned in this context can be applied to various vibrational scenarios.

Perhaps one of the most crucial principles in understanding vibration and energy is the conservation of energy. This fundamental law of physics explains how energy is transferred between different forms in a vibrational system without being created or destroyed. It's particularly important when analyzing the conversion between potential and kinetic energy in oscillating systems.

By mastering these prerequisite topics, students can develop a comprehensive understanding of vibration and energy. The concept of simple harmonic motion provides the foundational mathematics and physics behind vibrations. Knowledge of rotational kinetic energy and angular momentum extends this understanding to more complex systems. Electric potential and potential energy concepts offer insights into energy storage and transfer in electrical and mechanical systems. Finally, the principle of energy conservation ties everything together, allowing for a holistic analysis of energy transformations in vibrational systems.

Each of these topics builds upon the others, creating a interconnected web of knowledge that's essential for tackling advanced concepts in vibration and energy. Whether you're studying mechanical oscillations, wave propagation, or quantum mechanical vibrations, these fundamental principles will serve as crucial building blocks. By investing time in thoroughly understanding these prerequisites, students will find themselves well-equipped to explore the fascinating world of vibration and energy in greater depth and complexity.