Sign In
Join for Free
 flag-ca

Torque and Rotational Inertia: Foundations of Rotational Motion
Dive into the essential physics concepts of torque and rotational inertia. Understand their crucial role in rotating objects, from machinery to celestial bodies. Build a strong foundation for advanced mechanics and engineering applications.

  1. Intros0/2 watched
  2. Examples0/13 watched
  1. 0/2
  2. 0/13
Now Playing:Torque and rotational inertia – Example 0a
Intros
0/2 watched
  1. Definition of "Torque"
  2. Rotational Inertia
Examples
0/13 watched
  1. A person exerts a force of 45N on the handle of a door 65cm wide.
    1. What is the magnitude of the torque if the force is exerted perpendicular to the door?

    2. What is the magnitude of the torque if the force is exerted at a 35°?

Torque and rotational inertia 
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • Definition of Torque
  • Translational equilibrium Vs. Rotational equilibrium
  • Rotational Inertia
  • Moment of inertia of uniform objects

Notes:


Torque

  • To have better understanding of the meaning of “torque”, let’s try the following activity and compare the motion of object as different forces are exerted.
  • A ruler is placed on a horizontal flat surface.

    • (a) The force is applied at the center of mass

Torque and Rotational Inertia

    \quad The whole object (ruler) will accelerate in the direction of the force exerted.

    (b) The force is applied away from the center of mass

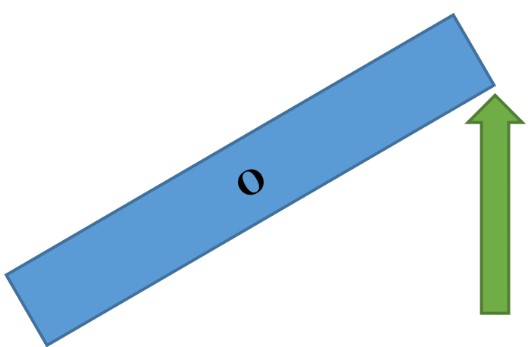
Torque and Rotational Inertia

The whole object (ruler) will rotate about the center of mass.

Torque and Rotational Inertia


As the result of exerting force, the object will rotate about the “Pivot” or “Axis of Rotation”.

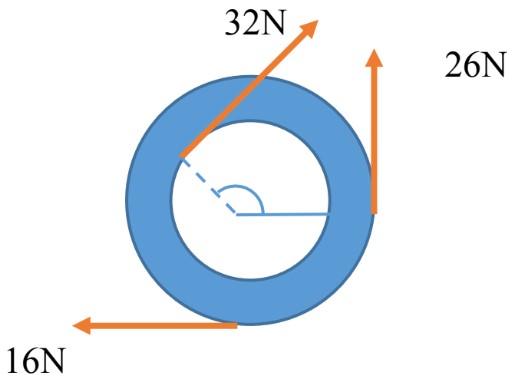
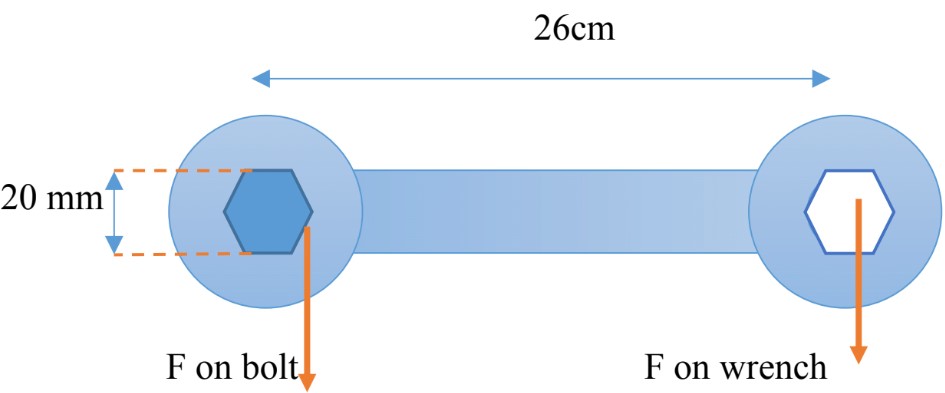
Therefore, we can define Torque as the “Turning Effect of a Force”.

Torque is represented by the Greek letter τ\tau and the standard unit is N.m.N.m.


Conclusion:
  • Force causes acceleration; F=maF=ma

  • Torque causes angular acceleration: τ=rFsin⁡θ  \tau = r F \sin \theta \; (vector quantity)
    θ\theta : angle between r r and F F
    r r : distance between the pivot and point at which the force is exerted on.

Torque and Rotational Inertia


τ ∝ r \tau \, \propto \, r : the further the force, the bigger the torque
τ ∝ θ \tau \, \propto \, \theta : the larger the angle, the bigger the torque 

The object could be in Translational Equilibrium and Rotational Equilibrium;

∑F=0 \sum F = 0 \qquad \qquad “Translational Equilibrium”   ⇒  \; \Rightarrow \, acceleration is zero
∑τ=0 \sum \tau = 0 \qquad \qquad “Rotational Equilibrium”   ⇒  \; \Rightarrow \, angular acceleration is zero


Rotational Inertia

Let’s consider a mass m rotating in a circle of radius r about a fixed point. The object is going to experience tangential and angular acceleration.

Torque and Rotational Inertia

I=mr2I = mr^{2} \quad (scalar quantity) Unit: kg.m2


“Rotational Inertia represents the resistance to angular acceleration”

  • Large Rotational Inertia: the mass of the object is distributed far from the axis of rotation.
    Objects with larger Rotational Inertia are harder to get rotating and harder to stop rotating.
  • Small Rotational Inertia: the mass of the object is distributed close to the axis of rotation.


I=mr2I = mr^{2} \qquad (single mass rotating of a single radius)
I=∑mr2  I = \sum mr^{2} \enspace \; (multiple individual masses rotating in circles of different radius)


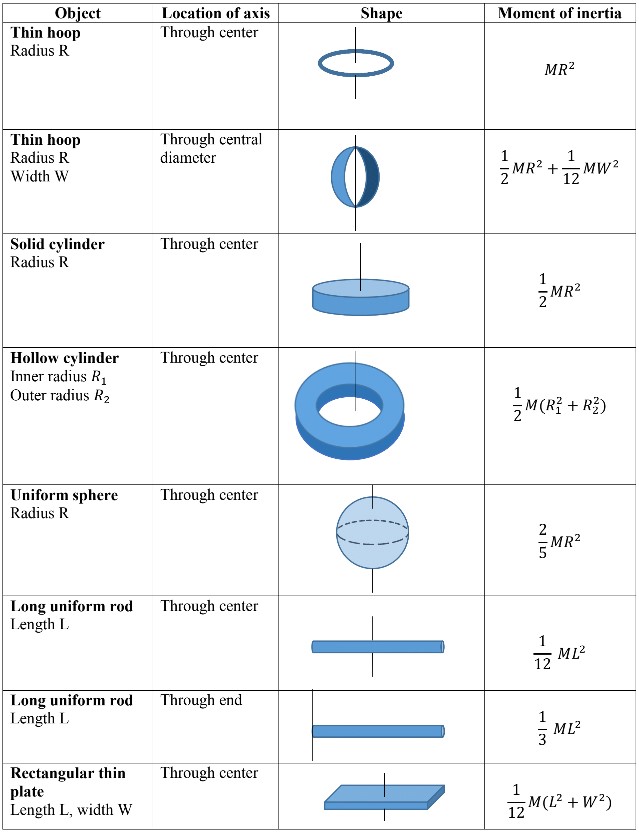
  • Moment of inertia for objects of uniform composition is constant;

Torque and Rotational Inertia
Concept

Introduction

Torque and rotational inertia are fundamental concepts in physics that play a crucial role in understanding the motion of rotating objects. Torque, often described as the rotational equivalent of force, measures the tendency of a force to cause an object to rotate around an axis. Rotational inertia, on the other hand, represents an object's resistance to changes in its rotational motion. The introduction video provided offers a comprehensive overview of these concepts, serving as an essential starting point for students and enthusiasts alike. By watching this video, viewers can gain a solid foundation in understanding the principles of torque and rotational inertia, which are vital in various fields of physics and engineering. These concepts have numerous real-world applications, from the design of machinery and vehicles to the analysis of celestial bodies' movements. Mastering torque and rotational inertia is crucial for anyone pursuing a career in physics, engineering, or related disciplines, as they form the basis for more advanced topics in mechanics and dynamics.

FAQs

  1. What is the difference between torque and force?

    Torque is the rotational equivalent of force. While force causes linear motion, torque causes rotational motion. Torque is calculated as the product of force and the perpendicular distance from the axis of rotation to the line of action of the force. Unlike force, which is measured in Newtons, torque is measured in Newton-meters (N·m).

  2. How does rotational inertia affect an object's motion?

    Rotational inertia, also known as moment of inertia, affects an object's resistance to changes in its rotational motion. Objects with higher rotational inertia require more torque to change their angular velocity. This property depends on both the mass of the object and how that mass is distributed relative to the axis of rotation.

  3. Why do figure skaters pull their arms in during a spin?

    Figure skaters pull their arms in during a spin to decrease their rotational inertia. According to the conservation of angular momentum, as the skater's rotational inertia decreases, their angular velocity must increase to maintain constant angular momentum. This results in the skater spinning faster without additional energy input.

  4. How is torque applied in everyday life?

    Torque is applied in many everyday situations. Examples include opening a door (applying force to the handle), using a wrench to tighten a bolt, pedaling a bicycle, and turning a steering wheel. In each case, a force is applied at a distance from a pivot point to create a rotational effect.

  5. What is the relationship between torque and angular acceleration?

    The relationship between torque and angular acceleration is described by the rotational form of Newton's Second Law: τ = Iα, where τ is torque, I is the moment of inertia, and α is angular acceleration. This equation shows that for a given torque, objects with larger moments of inertia will experience less angular acceleration, and vice versa.

Prerequisites

Understanding the concept of torque and rotational inertia is crucial in physics, but it's essential to have a solid foundation in prerequisite topics. One of the most important prerequisites for grasping torque and rotational inertia is Newton's second law of motion. This fundamental principle serves as the cornerstone for understanding how forces affect the motion of objects, including rotational motion.

Newton's second law of motion, typically expressed as F = ma, describes the relationship between force, mass, and acceleration in linear motion. However, when dealing with rotational motion, we need to adapt this principle to account for the unique characteristics of rotating objects. This is where the concept of Newton's Second Law for rotation comes into play, forming a bridge between linear and rotational dynamics.

By understanding Newton's second law, students can more easily grasp how torque (the rotational equivalent of force) affects the angular acceleration of an object. Just as force causes linear acceleration in Newton's second law, torque causes angular acceleration in rotational motion. This parallel helps students draw connections between linear and rotational physics, making the transition to more complex rotational concepts smoother.

Moreover, the concept of mass in Newton's second law translates to rotational inertia (also known as moment of inertia) in rotational dynamics. Rotational inertia represents an object's resistance to rotational acceleration, much like how mass represents an object's resistance to linear acceleration. By understanding the relationship between force and mass in linear motion, students can more easily comprehend the relationship between torque and rotational inertia in rotational motion.

The mathematical form of Newton's Second Law for rotation (τ = Iα, where τ is torque, I is rotational inertia, and α is angular acceleration) mirrors the structure of F = ma. This similarity helps students recognize the parallels between linear and rotational motion, reinforcing their understanding of both concepts.

In conclusion, a solid grasp of Newton's second law of motion is invaluable when studying torque and rotational inertia. It provides the necessary framework for understanding how forces and motion work in both linear and rotational contexts. By mastering this prerequisite topic, students will find themselves better equipped to tackle the complexities of rotational dynamics, ultimately leading to a more comprehensive understanding of physics as a whole.