Superposition of waves
0/3
Intros
0/2
Examples
Lessons
- Sketch the result of the following superposition cases on the dashes line. Identify the constructive and destructive interference and give the value of the resultant amplitude.
- Bathtub water is sloshed back and forth with a frequency of 0.20Hz to produce standing waves. Suppose the standing wave produced is 120 cm long. Calculate the velocity of the water waves.
Topic Notes
In this lesson, we will learn:
- Waves superposition
- Waves interference
- Standing waves
Notes:
Superposition (When two or more waves travelling though one another)
- As waves pass through each there is no change in:
Amplitude, direction, speed, frequency, wavelength - The displacement at the point where they meet is the sum of the displacements.
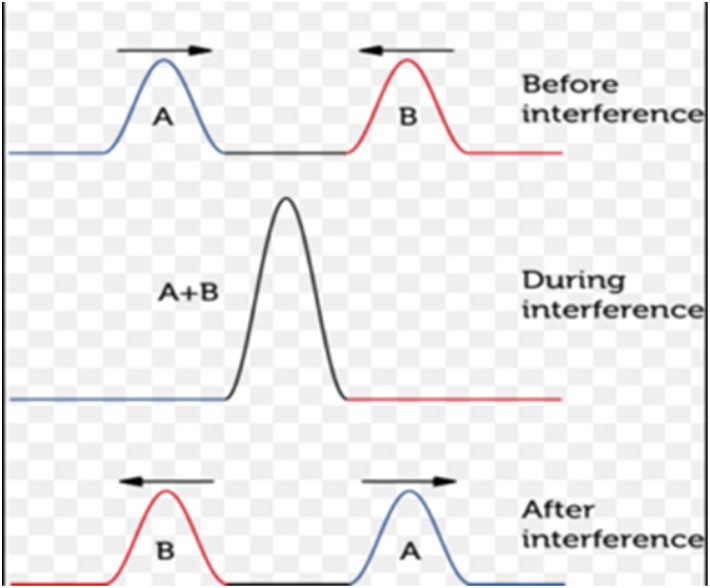
- When pulses pass through one another superposition takes place.
Interference
- When pulse meet at a point at the same time interference occurs.
- Interference is the result of the superposition of two or more waves (the point where they meet).
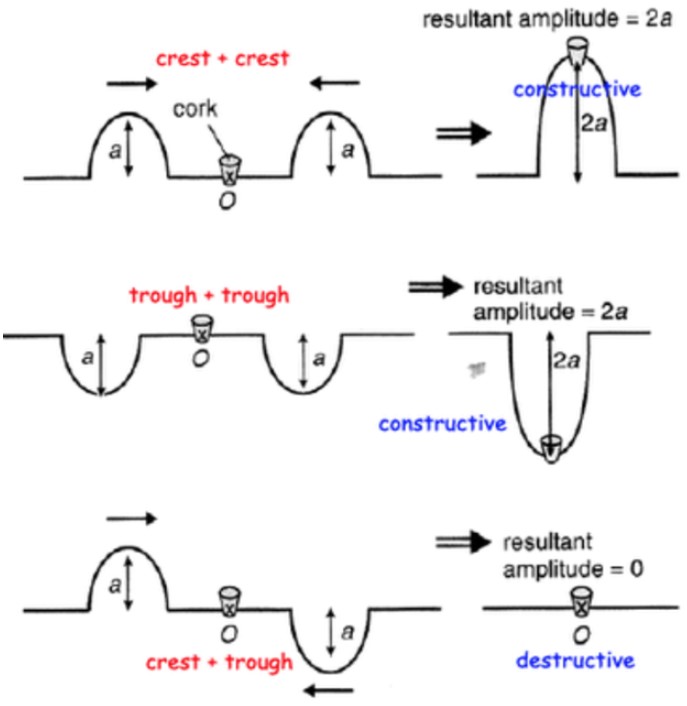
- Constructive interference: waves displacement are in the same direction, displacements add up, maximum displacement (ANTINODE)
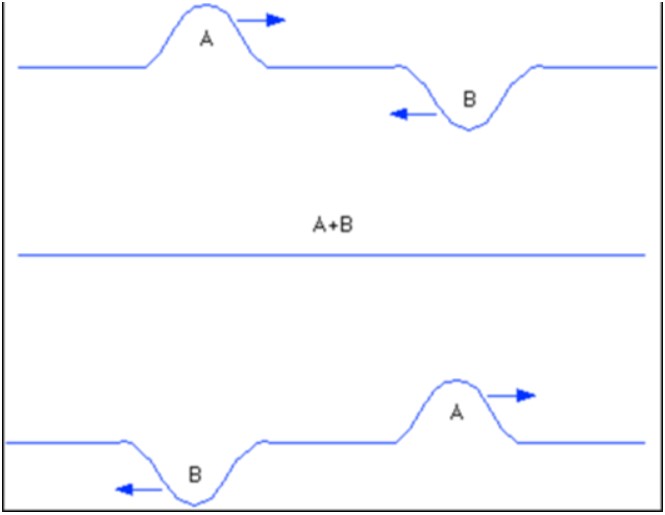
- Destructive interference: waves displacement are in the opposite direction, displacements cancel out, zero displacement (NODES)
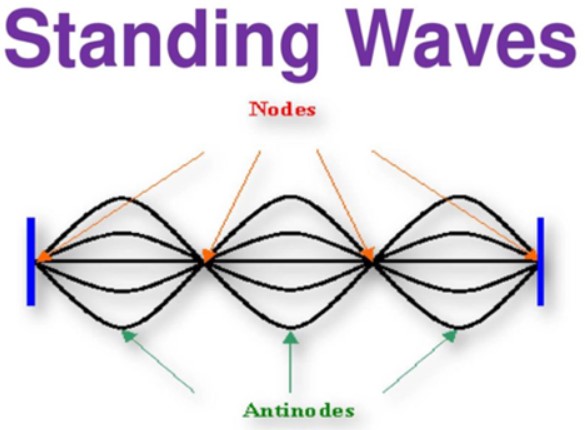
Standing waves
- When a string is plugged pulses travel back and forth, reflecting from the ends producing a complex of superposition called standing waves. Superimposed waves can produce standing waves.
