Rotational Vs. translational kinematics

In this lesson, we will learn:

• Definition of Rotational Motion, Rigid Object and The Axis of Rotation.
• Translational-Rotational Analogues
• Tangential Acceleration Vs. Centripetal Acceleration
• Rotational Kinematics Equations
• Rolling Without Slipping Motion

Notes:


Rotational Motion

• To explain the rotational motion, we need to consider a rigid object.


• A rigid object: it is an object with a definite shape, the particles composing the object are at a fixed position relative to one another.


• When an object rotates, all the points composing the object move in a circle.


• Axis of Rotation: The center of all circles lie on a line called Axis of Rotation, which is perpendicular to the page.

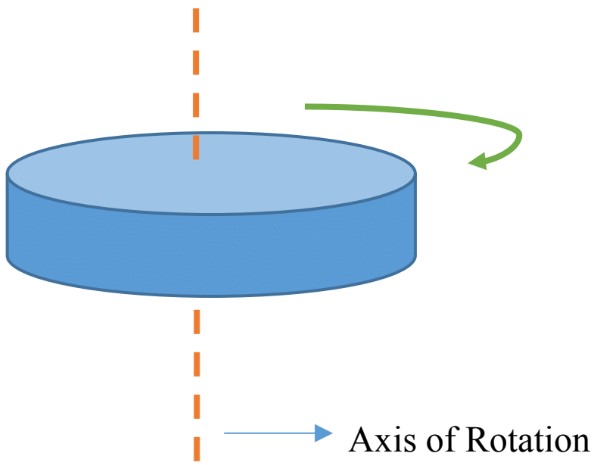
• Through rotation, the object changes position and moves through different angles; $\theta _{i}, \theta _{f}$


$\Delta \theta = \theta_{f} - \theta_{i}$
$\qquad \Delta \theta$: Change in position, angular displacement (radians)
$\qquad \theta_{f}$: Final position
$\qquad \theta_{i}$: Initial position 


• Similar to translational motion velocity is defined as a change in position over time elapsed;

$\large w = \frac{\Delta \theta}{\Delta t}$
$w$: angular velocity (radians/sec)

• Similarly, the acceleration is defined as a change in velocity over time elapsed;

$\propto \, =$ $\large \frac{\Delta w}{\Delta t}$
$\propto$: angular acceleration (radians/sec²)

Translational-Rotational Analogues

• Each point of a rotating object has a linear velocity and a linear acceleration, so we have to relate the linear quantities to the angular quantitates.

$v =$ $\large \frac{\Delta l}{\Delta t}$ $=$ $\large \frac{r \Delta \theta }{\Delta t}$ $= rw$
$v = rw \,$ (1)

$a =$ $\large \frac{\Delta v}{\Delta t}$ $=$ $\large \frac{r \Delta w}{\Delta t}$ $= r \propto$
$a = r \propto \,$ (2)

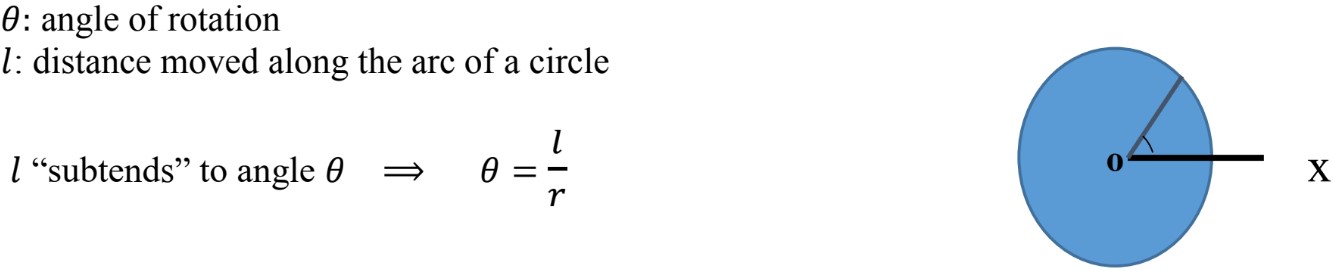
Tangential Acceleration Vs. Centripetal Acceleration

In rotational motion, we have to consider the two components of acceleration,

$a_{r}$; tangential component, that changes the magnitude of the velocity and it is tangent to the direction of motion;

$a_{r} = r \propto$
$a_{c}$; centripetal competent, that changes the direction of velocity and is directed towards the center (caused by centripetal force);

$a_{c} =$ $\large \frac{v^{2}}{r}$
To find the total acceleration we can find the magnitude of the acceleration using the Pythagoras theorem;

$a^{2}_{total} \, = \, a\frac{2}{T} \, +\, a\frac{2}{c}$
$a_{total} \, = \, \sqrt{a^{2}_{T} \, + \, a^{2}_{c} }$

Rotational Kinematics Equations
The following table compares the rotational kinematics equation to the translational kinematics equation.



Conversion Factor
It is very common in rotational motion to measure the angular velocity in round per minutes (rmp), in order to convert to the standard unit of radians per second (rad/s), we use the following the conversion factor;

rmp × $\frac{2 \pi \; rad \; / \; rev}{60\;sec\;sec\; / \; min}$ rad/s

Rolling Without Slipping
There are many examples in everyday life, where the object rolls but it does not slip.
Examples: rolling ball, rolling wheel.
Rolling without slipping depends on the static friction between the rolling object and the floor.
In this case, we have to consider both rotational and translational motion. To relate these two types of motion, use $v = rw$ (where $r$ is the radius).

As the following diagram represents, the wheel is rolling (Rotational Motion) to the right and at the same time, the center of gravity is changing position (Translational Motion).


$\large \frac{d}{t}$ $=$ $\large \frac{r \Delta \theta}{t}$ $\quad \Rightarrow \quad v = rw$

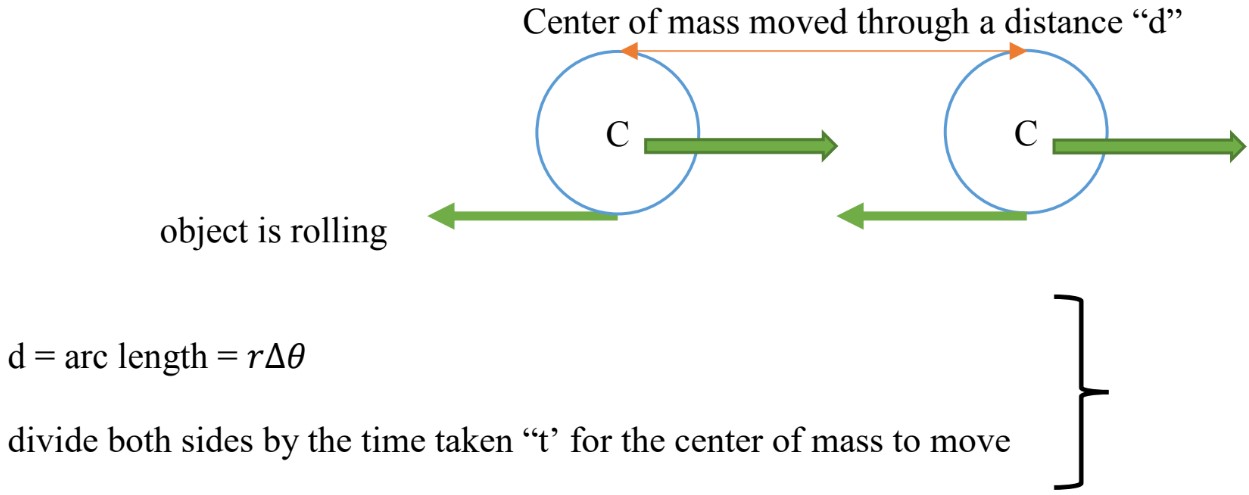
$v$: Center of mass speed
$r$: Radius 
$w$: Angular speed about the center of mass