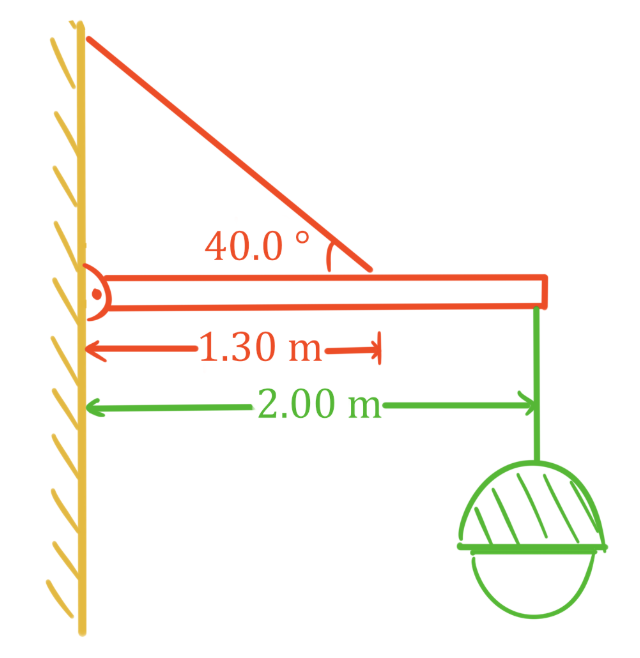
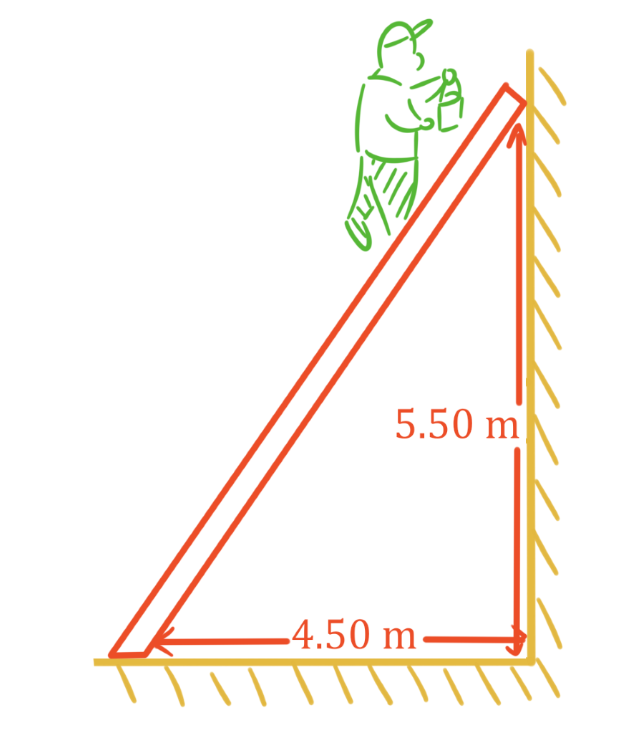
In this lesson, we will learn:
- Solving statics problems using both translational and rotational equilibrium
Notes:
- An object or group of objects that are not moving are in static equilibrium.
- In static equilibrium, the conditions for both translational and rotational equilibrium must be met.
or equivalently:
and
sum of all forces, in newtons (N)
sum of all force components in x direction, in newtons (N)
sum of all force components in y direction, in newtons (N)
Torque
: torque, in newton meters (N·m)
component of force perpendicular to , in newtons (N)
distance from point of rotation, in meters (m)
Conditions for Rotational Equilibrium
N·m
or simpler equation:
total = total
sum of all torques, in newton meters (N·m)
total : magnitude of all torques in the clockwise direction, in newton meters (N·m)
total : magnitude of all torques in the counterclockwise direction, in newton meters (N·m)