Solving two dimensional vector problems

0/1

Introduction to solving two dimensional vector problems
- Overview of trigonometry strategies for different types of vector problems
- Definition of the law of sines and the law of cosines

0/6

Use the law of sines to solve triangles
1. Find the length of side c
2. Find the angle θ
Use the law of cosines to solve triangles
1. For the following triangle:
  1. Find the length of the unknown side.
  2. Find the angle θ
2. A paper airplane is thrown 11.0 m [W], then thrown 14.0 m, then 16.0 m. The final throw returns it to its original position. Find the angle of the 14.0 m throw.
Solve a vector word problem using the laws of sines and cosines

To get to school, Pauline leaves her house and walks due east 1.40 km, then takes a shortcut by walking 0.650 km [35° S of E] through a park. Find her displacement from home to school.
Solve a difficult vector triangle using geometry

Solve the equation $\vec{A} + \vec{B} = \vec{C}$ .

In this lesson, we will learn:

How to solve two dimensional vector problems using the law of sines and the law of cosines

Notes:

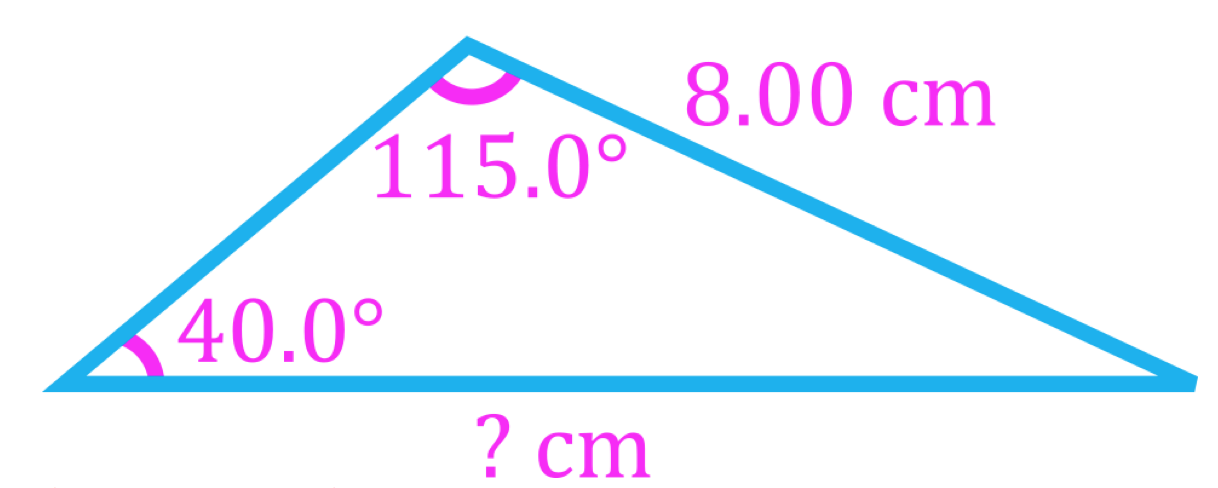
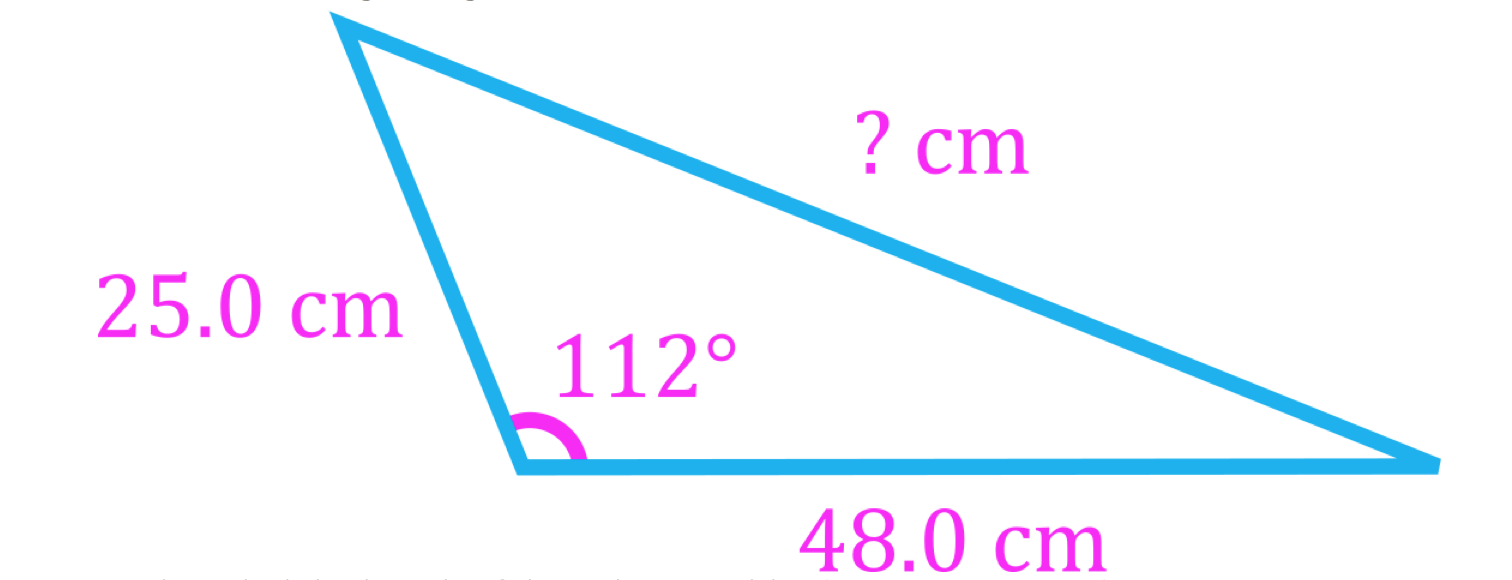
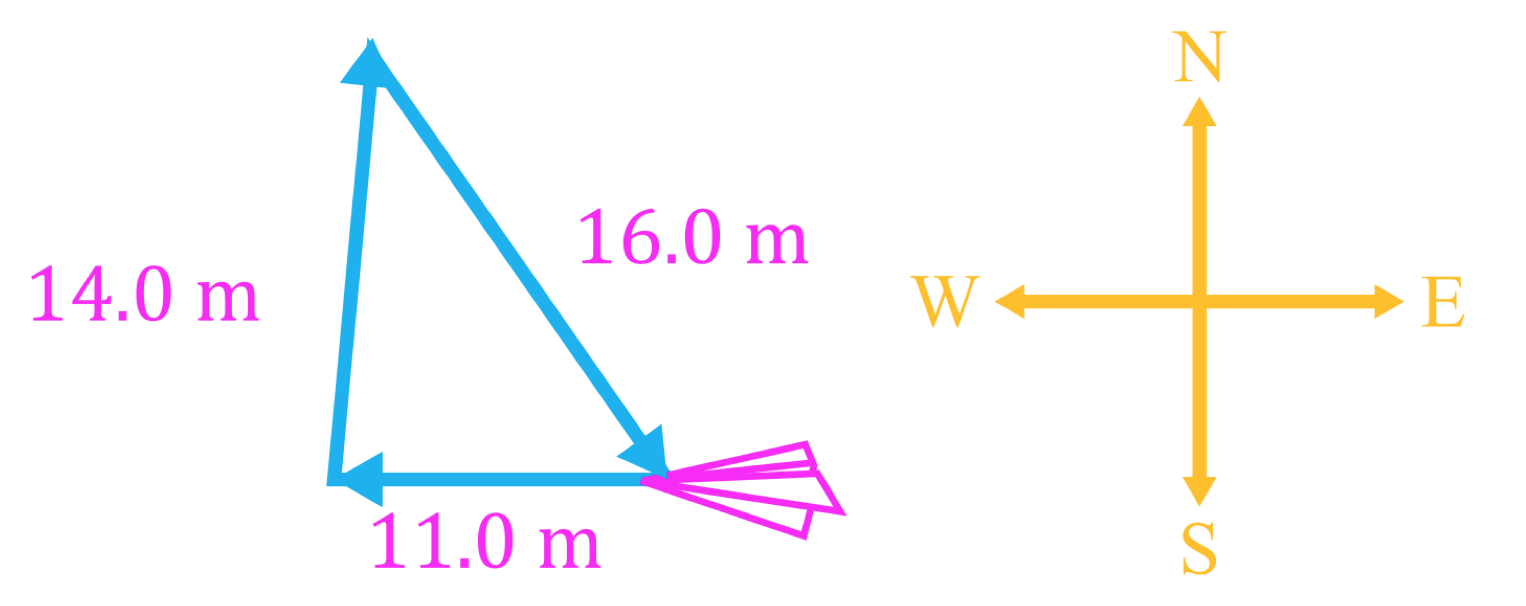
Often, vector equations in physics problems result in vector triangles which can be solved using trigonometry
At least three pieces of information are needed to solve a triangle, which can be three side lengths (SSS), two side lengths and one angle (SSA, SAS), or one side length and two angles (SAA, ASA).

Knowing three angles (AAA) does not let you solve a triangle since you will not be able to solve for the side lengths. There is no way to know the size of the triangle without more information.

You can always solve a triangle that you know four or more pieces of information about.
Vector triangles that do not contain right angles can be solved either by breaking vectors into their components or using the law of sines and the law of cosines, which are trigonometric laws that apply to all triangles

Law of Sines

$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}$
a,b,c: length of sides a,b,c
A,B,C: angles opposite sides a, b, c

Law of Cosines

$c^2 = a^2 + b^2 - 2ab \,cosC$