Position, velocity, acceleration and time

In this lesson, we will learn:

• The definition and difference between Displacement and Distance
• The definition and difference between Speed and Velocity
• Definition of Acceleration
• Position Vs. Time graph
• Velocity Vs. Time graph
• Acceleration Vs. Time graph

Notes:

Displacement Vs. Distance


Displacement: it is defined as change in position, $\Delta X = X_{f}-X_{i}$.
It is a vector quantity, it has both magnitude and direction.


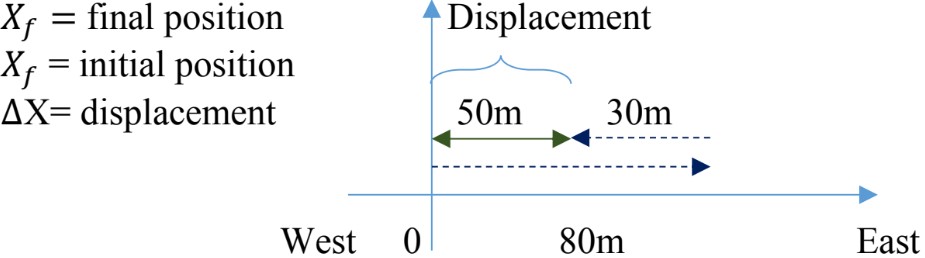
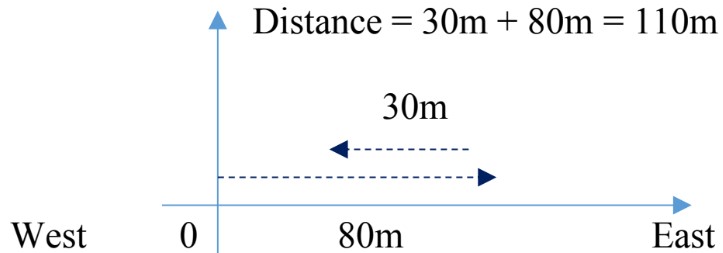
Distance: the length of the path covered between two points. It is also defined as the magnitude of displacement between two positions.
It is a scalar quantity, it has only magnitude.



Example:

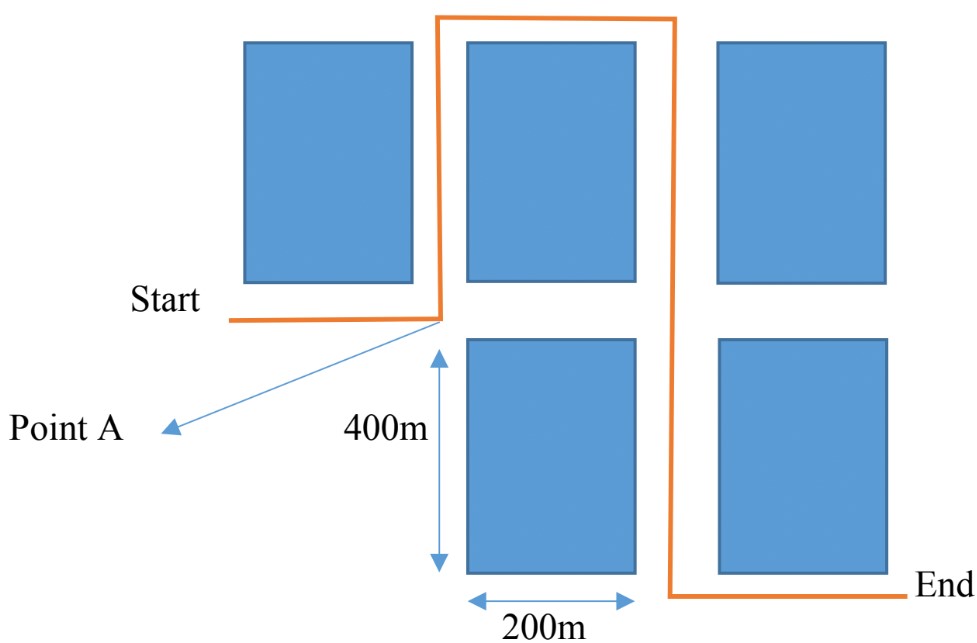
An athlete is running around a rectangular field as shown below with a length of 240 cm and width of 120cm.



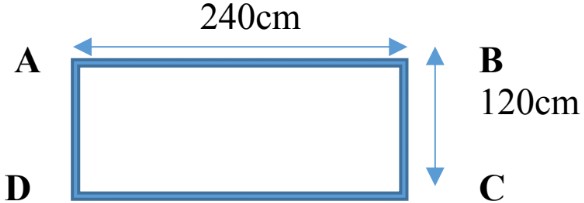
Calculate distance and displacement covered for the following paths;

1. $\,A \,$→$\, B$
   Distance (d): total distance covered form A to B is 240cm.
   Displacement $(\Delta X): \Delta X= X_{f} - X_{i} = AB$ = 240cm



2. $\,A \,$→$\, B \,$→$\, C$
   Distance (d): total distance covered: 240cm + 120cm = 360cm
   Displacement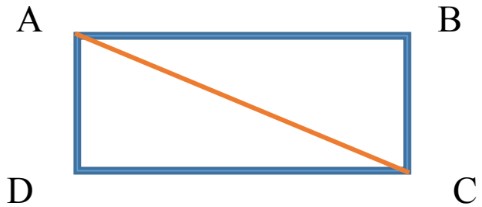 $(\Delta X): \Delta X= X_{f} - X_{i} = X_{c} - X_{A} = AC$
   
   
   To find the length of AC, we have to use Pythagoras theorem:
   
   $(AC)^{2}=(AB)^{2}+(BC)^{2}$
   $(AC)^{2}=(240cm)^{2}+(120cm)^{2}$
   $(AC)^{2}=57600cm^{2} + 14400cm^{2}$
   $(AC)$ = 268.33 cm
   
   $\Delta X = AC = 268.33 \, cm$



3. $\,A \,$→$\, B \,$→$\, C \,$→$\, D$
   
   Distance (d): $AB + BC + CD$ = 240cm + 120cm + 240cm = 600cm
   Displacement $(\Delta X):\Delta X = X_{f} - X_{i}=X_{D}- X_{A}= A_{D}$ = 120cm



4. $\,A \,$→$\, B \,$→$\, C \,$→$\, D \,$→$\, A$
   
   Distance (d): $AB + BC + CD + AD$ = 240cm + 120cm + 240cm + 120cm = 720cm
   Displacement $(\Delta X):\Delta X=X_{f}-X_{i}=X_{A}-X_{A}=$ 0

Velocity Vs. Speed



Average Velocity: change position divided by the time taken; $\large V_{avg} = \frac{\Delta X} {\Delta t} = \frac{X_{f} - X_{i}} {t_{f} - t_{i}}$
It is a vector quantity which has both magnitude and direction.

Average Speed: total distance travelled divided by the time taken; $\large S_{avg} = \frac{d} {t}$
It is a scalar quantity which has only magnitude.

Instantaneous Velocity: velocity at an instant of time.

Instantaneous Speed: speed at an instant of time.


Acceleration

An object whose velocity is changing is said to be accelerating, it specifies how rapidly the velocity of the object is changing.

Average Acceleration: it is defined as the change in velocity divided by the time taken.
It is a vector quantity which has both magnitude and direction.

$\large a_{avg} = \frac{\Delta V} {\Delta t} = \frac{V_{f} - V_{i}} {t_{f} - t_{i}}$

Instantaneous Acceleration: it is defined as the acceleration of the object at instant of time.

Standard unit of acceleration: $\large \frac{m} {s^{2}}$


Graphical Analysis

Position Vs. Time Graph

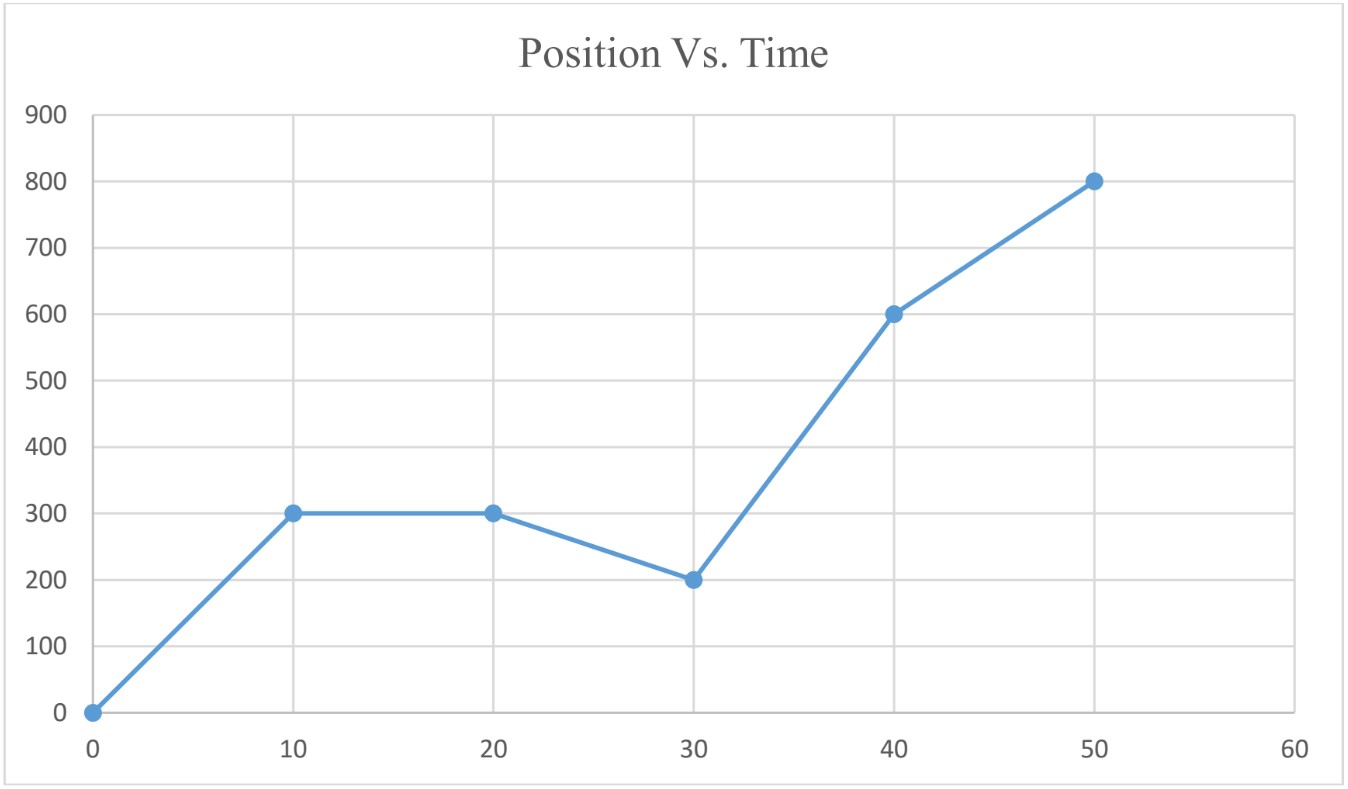
The following graph represents the position Vs. time graph for an object moving with constant velocity.



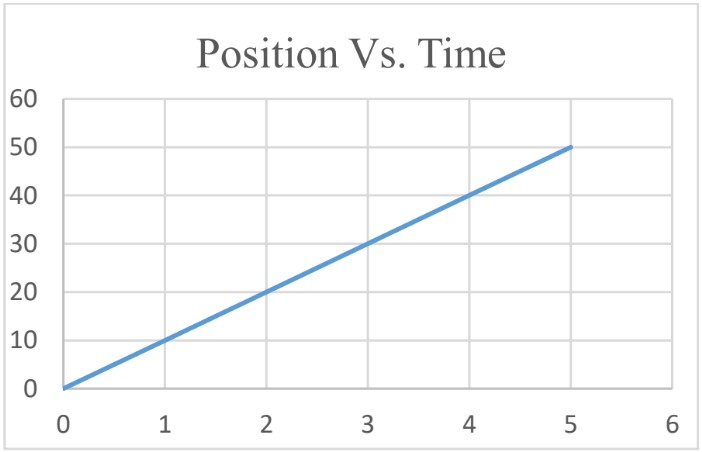
Using position Vs. time graph we can find the following quantitates;

1. Average velocity
   To find $V_{avg}$ , find the slope of the graph.
   
   $V_{avg} = slope = \frac{Rise} {Run} =$ $\large \frac{x_{2} - x_{1}} {t_{2} - t_{1}} = \frac{\Delta X} {\Delta t}$
   
   Example;
   
   $V_{avg} = slope = \frac{Rise} {Run} =$ $\large \frac{50 - 10} {5 - 1} = \frac{40} {4}$ = 10m/s
   
   


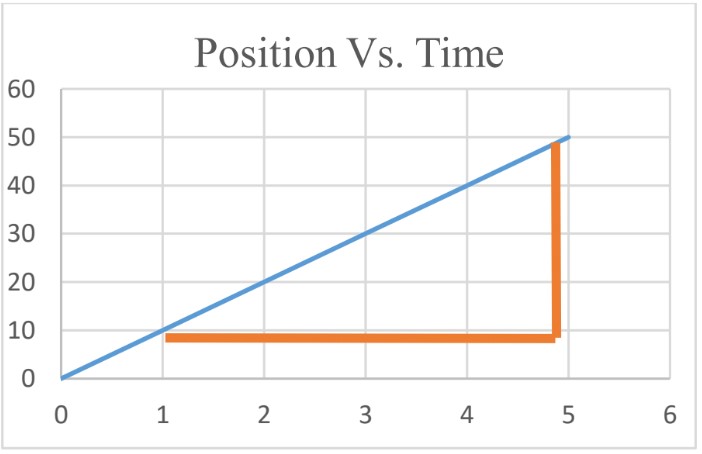
2. Instantaneous Velocity
To find instantaneous velocity from the graph, calculate the slope of the graph at that instant of time.

$V_{inst}$ at $t = 2s, V_{inst} = slope =$ $\large \frac{20- 0} {2- 0} =$ 10 m/s

Note: for bodies moving with constant velocity; $V_{inst}=V_{avg}$

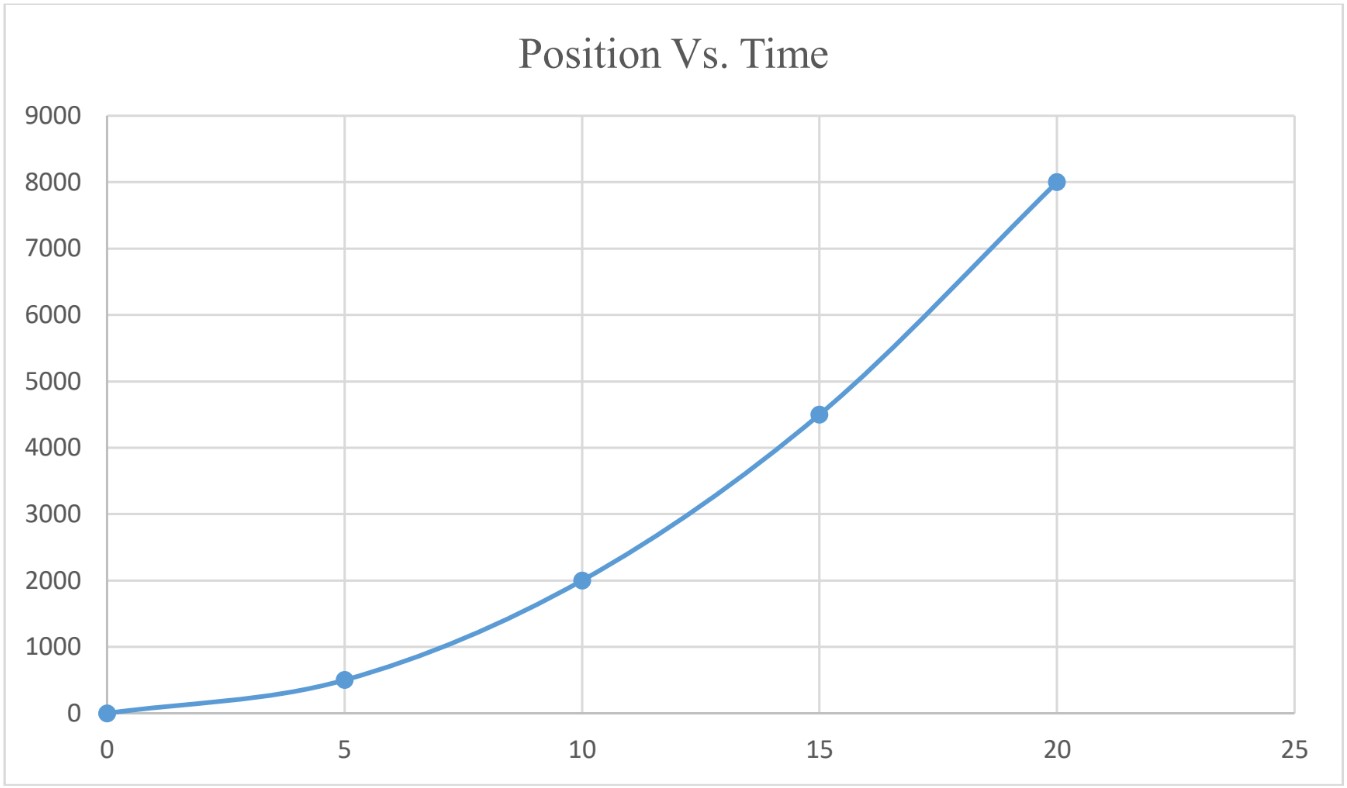
The following graph represents position Vs. time graph for an object moving with variable velocity (velocity is NOT constant).

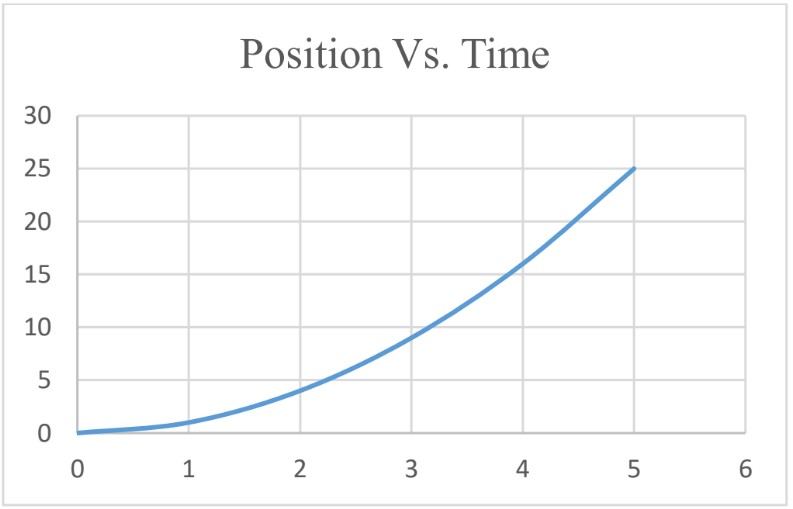
1. Average Velocity
   To find $V_{avg}$, find the slope of the graph.
   
   $V_{avg} = slope = \frac{Rise} {Run} =$ $\large \frac{x_{2} - x_{1}} {t_{2} - t_{1}} = \frac{\Delta X} {\Delta t}$
   
   
   
   
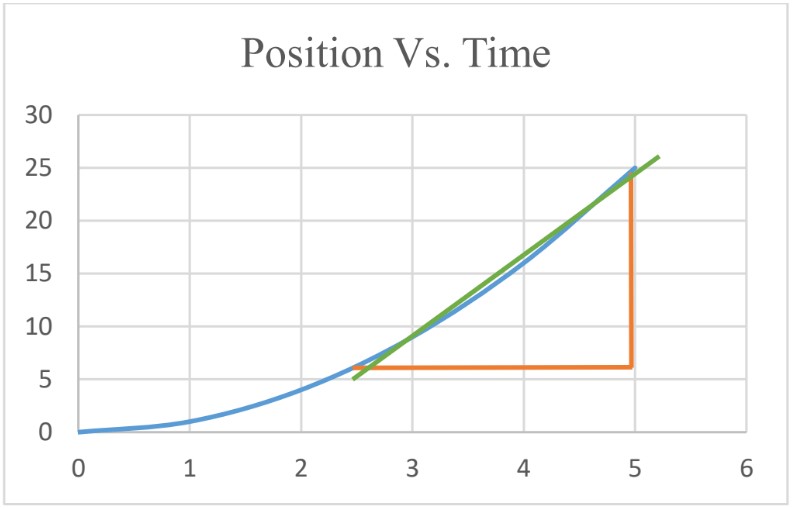
   $V$_{avg (2.8 s → 5.0s)} = slope =$\large \frac{Rise} {Run} = \frac{x_{2} - x_{1}} {t_{2} - t_{1}} = \frac{25 - 7.5} {5-2.8}$ = 7.95 m/s



2. Instantaneous Velocity
To find instantaneous velocity from the graph, calculate the slope of the graph at that instant of time. To do that, draw the tangent at that instant of time and calculate the slope of the tangent.




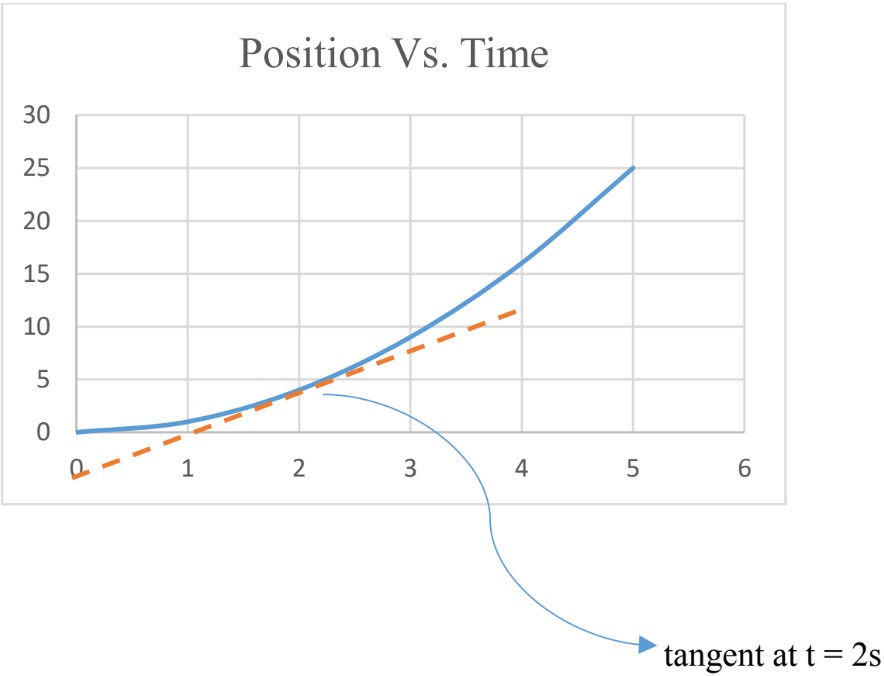
$V_{inst}$ at $t = 2s$

$V_{inst}$ = slope of the tangent =$\large \frac{Rise} {Run} = \frac{x_{2} - x_{1}} {t_{2} - t_{1}} = \frac{3.75 - 1.25} {2-1}$ = 2.5 m/s

Note: for bodies moving with variable velocity; $\large V_{inst} \neq V_{avg}$

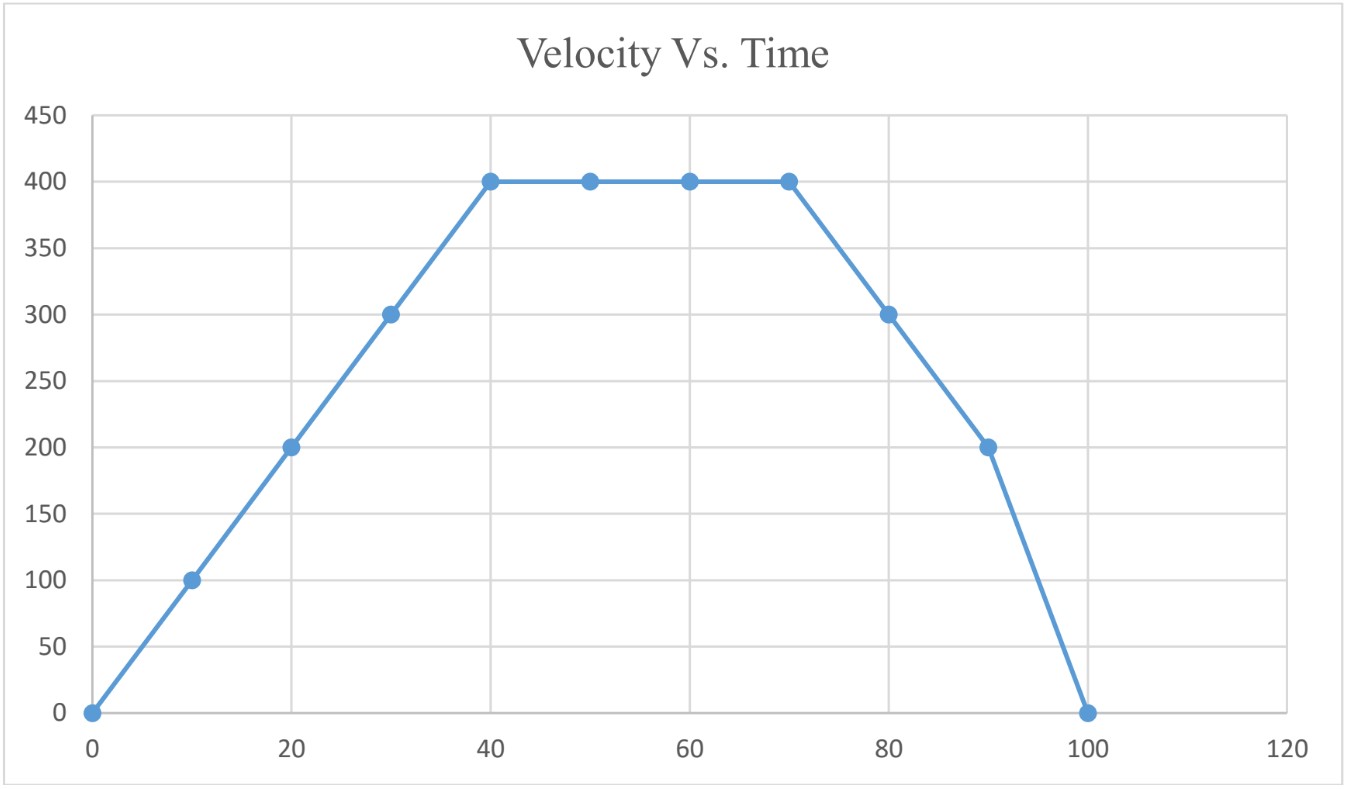
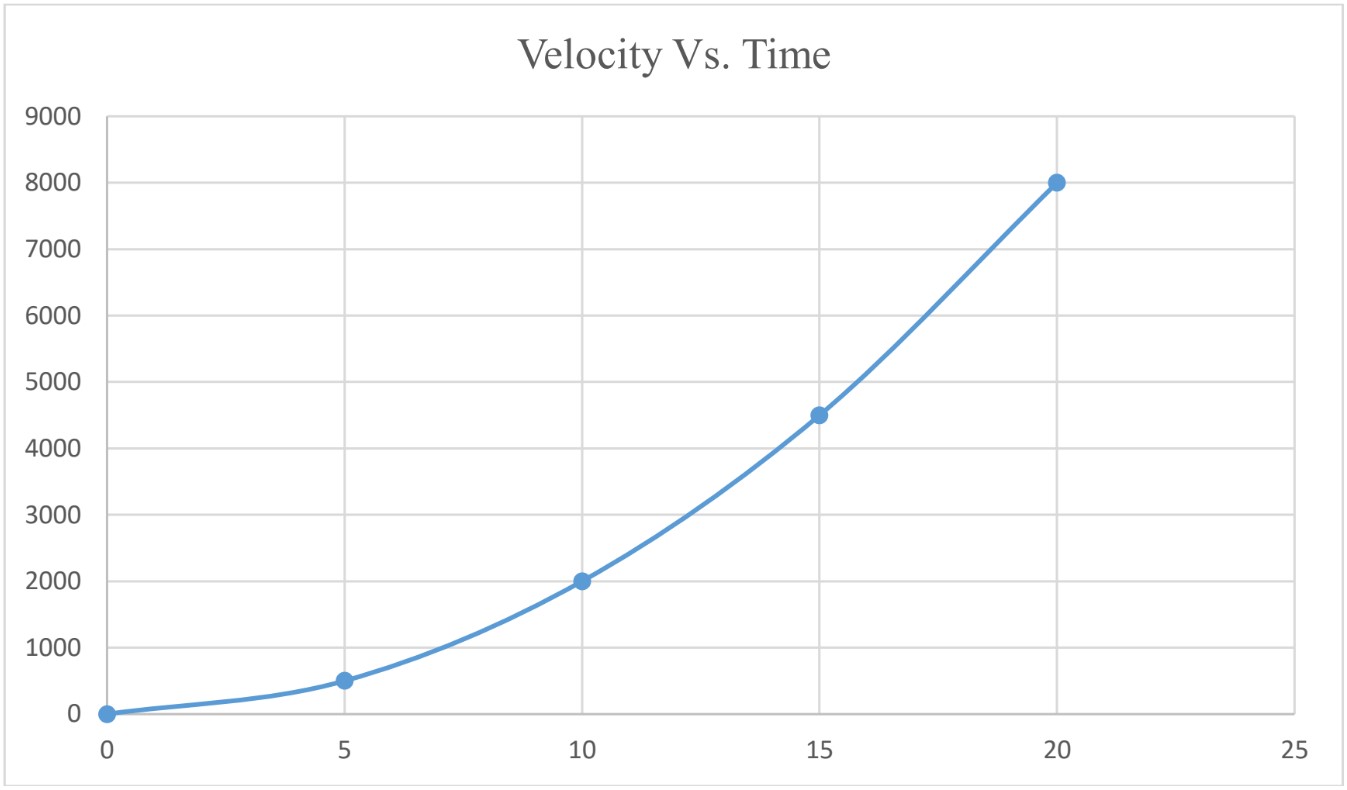
Velocity Vs. Time Graph

Using Velocity Vs, Time graph you can find;

1. Acceleration (slope)
2. Displacement (Area under graph)

Constant Acceleration

To find average acceleration from Velocity Vs. Time graph, calculate the slope of the graph.

For bodies moving with constant acceleration, $\large a_{avg} = a_{inst}$




$\large a_{avg}= a_{inst}$ = slope=$\large \frac{Rise} {Run} = \frac{V_{2} - V_{1}} {t_{2} - t_{1}} = \frac{50 - 10} {5-1} = \frac{40} {4}$ = 10 $\large \frac{m} {s^{2}}$


Variable Acceleration
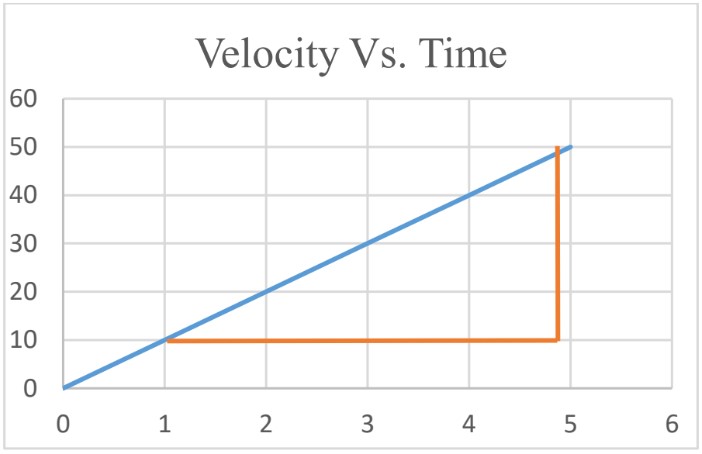
Average Acceleration
To find average acceleration from the graph, calculate the slope of the graph during the specific interval of time.




$\large a_{avg} = \,$ slope=$\large \frac{Rise} {Run} = \frac{V_{2} - V_{1}} {t_{2} - t_{1}} = \frac{25 - 5} {5-2} = \frac{20} {3}$ = 6.67 m/s²

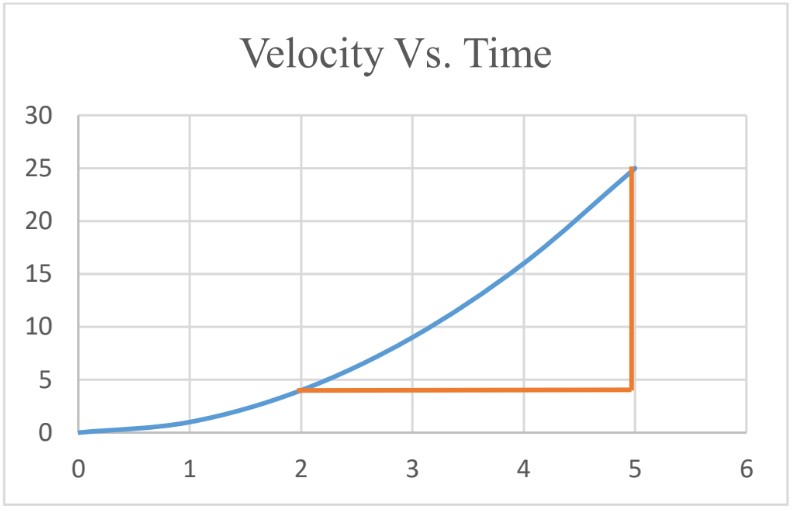
Instantaneous Acceleration
To find instantaneous acceleration from the graph, calculate the slope of the graph at that instant of time. To do that, draw the tangent at that instant of time and calculate the slope of the tangent.




$a_{inst}$ at $t = 2s$;

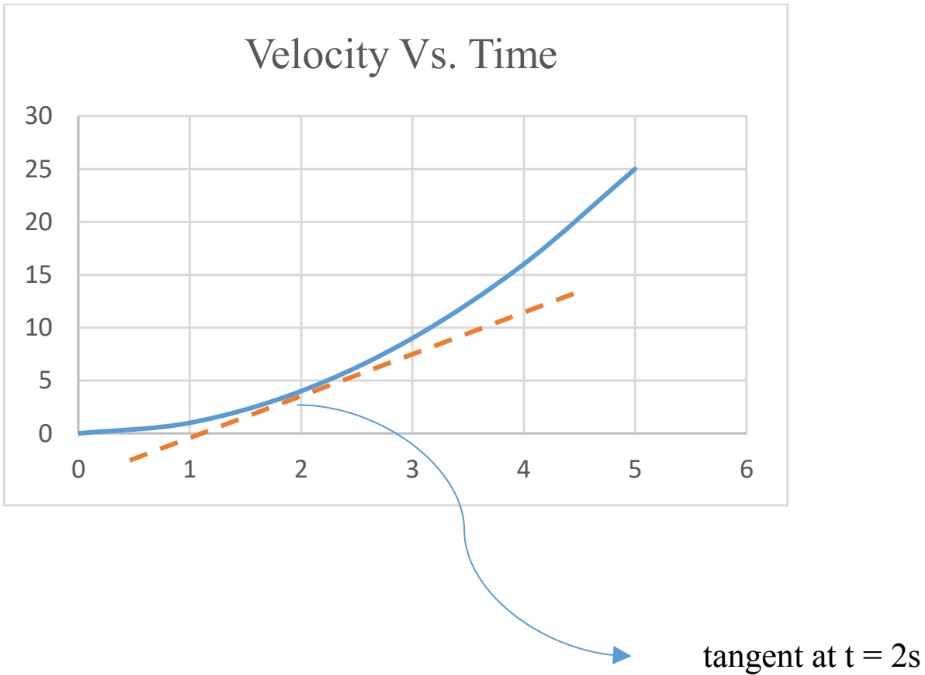
$\large a_{inst} = \,$ slope of the tangent =$\large \frac{Rise} {Run} = \frac{V_{2} - V_{1}} {t_{2} - t_{1}} = \frac{3.75 - 1.25} {2-1} =$ 2.5 m/s²

Note: for bodies moving with variable acceleration; $a_{inst} \neq a_{avg}$


Displacement as the Area Under the Graph
Using Velocity Vs. Time graph you can find the displacement by calculating the area under the graph.




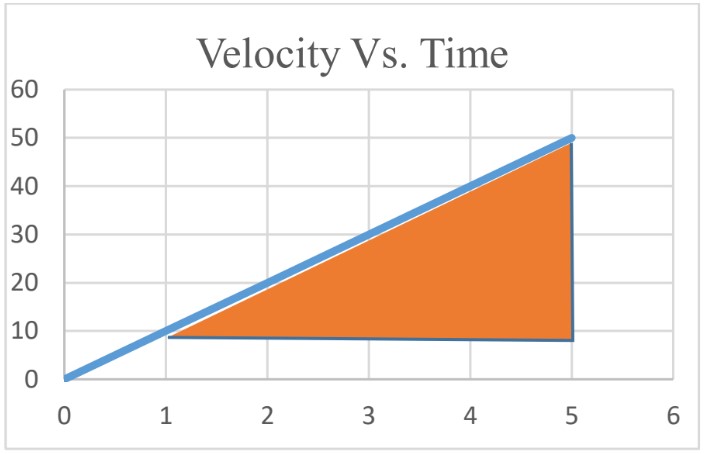
Displacement from 1s to 5s;

Area of a triangle = $\large \frac{1}{2}$ base × height = $\large \frac{1}{2}$ × 40 × 4 = 80m

Note: Since the motion is along a straight line, the displacement is equal to distance covered.

Let’s consider the following Velocity Vs. Time graph, where the object changes direction as it moves.




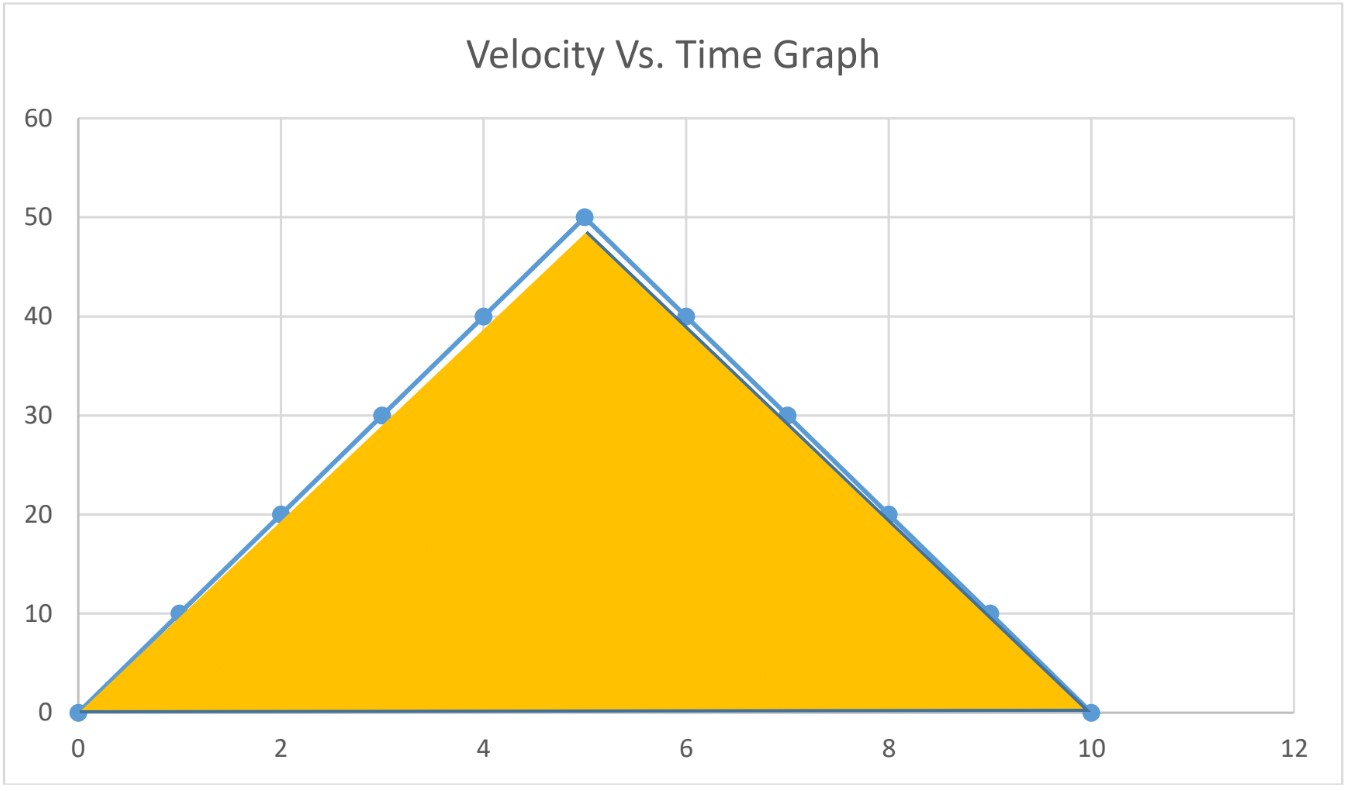
Total displacement; area under the graph
Area of a triangle = $\large \frac{1}{2}$ base × height = $\large \frac{1}{2}$ × 10 × 50 = 250m

Total distance covered; distance covered from 0s to 5s + distance covered from 5s to 10s
Total distance = 50m + 50m = 100m

Note: Distance and Displacement are different, since the object changed direction.