Sign In
Sign Up
flag-ca

Ohm's Law: The Foundation of Electrical Circuit Analysis
Master the fundamental relationship between voltage, current, and resistance. Learn to apply Ohm's Law in real-world circuits, from basic electronics to complex electrical systems.

  1. Intros0/2 watched
  2. Examples0/7 watched
  1. 0/2
  2. 0/7
Now Playing:Ohmslaw1 – Example 0a
Intros
0/2 watched
  1. Introduction to Ohm's Law:
  2. Introduction to Ohm's Law:
    What have we learned about voltage, current and resistance?
  3. Introduction to Ohm's Law:
    What does Ohm's Law tell us about circuits?
Examples
0/7 watched
  1. Solving for Current with a Single Resistor in Series


    Ohm's Law
    1. Find the current flowing in the circuit.

    2. If the battery is connected to the circuit for 30 seconds, how much charge passes through the resistor?
      1. 4.0 C
      2. 120 C
      3. 500 C
      4. 3000 C

Voltage
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • A review on the electric circuit and the main components: battery (voltage), closed wire path (current), and devices/resistors that use up electricity (resistance).
  • Also, a review on the main rules/methods we used to solve for each concept individually (voltage and Kirchhoffs Loop Rule; current and Kirchhoffs Junction Rule; resistance summation formulas)
  • What is the relationship between voltage, current, and resistance?
  • How to solve circuit problems for voltage, current, and resistance using Ohms Law which states that:
    • V=IR V=IR
    • And also, how to rearrange Ohms Law: V=IR V=IR ; I=VR I= \frac{V} {R} ; R=VI R= \frac{V} {I}

Notes:

  • Recall that: a circuit is a closed loop that charge flows within; the three main components of a circuit are voltage (provided by a battery source), current (the rate of flow of charge within the circuit wires), and resistance (a property of the electronic devices using up energy).
    • Voltage is measured in the unit volts (V) which is equal to Joules/Coulomb
    • Current is measured in the unit ampere (A) which is equal to Coulombs/Second
    • Resistance is measured in the unit ohm (Ω \Omega ) which is equal to Volts/Ampere

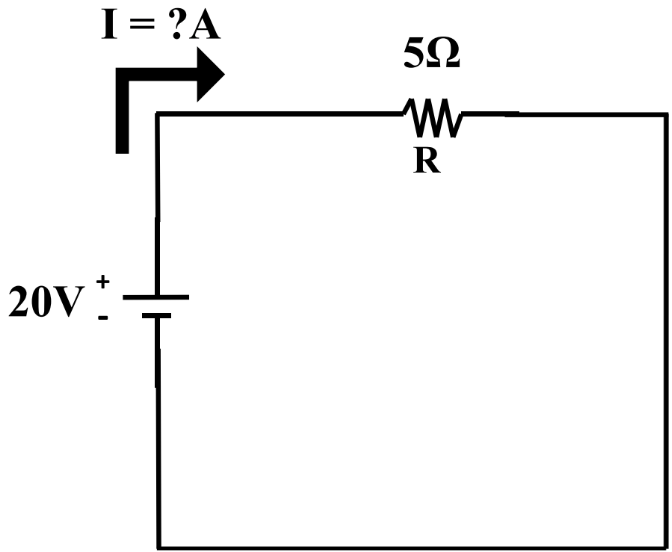
  • Ohms Law states that the voltage is equal to the current multiplied by resistance:
    • V=IR V=IR
    • For metals, resistance is constant and independent of voltage
    • Voltage is directly proportional to current (V∝I V \propto I)

  • The Ohms Law equation can be rearranged to solve for any of the three main concepts (voltage, current, resistance).
    • V=IR V=IR ; I=VR I= \frac{V} {R} ; R=VI R= \frac{V} {I}
    • The current coming out of a battery is dependent on the resistance of the circuit its connected to

  • Solving questions using Ohms Law requires a strong understanding of solving for the three main concepts individually
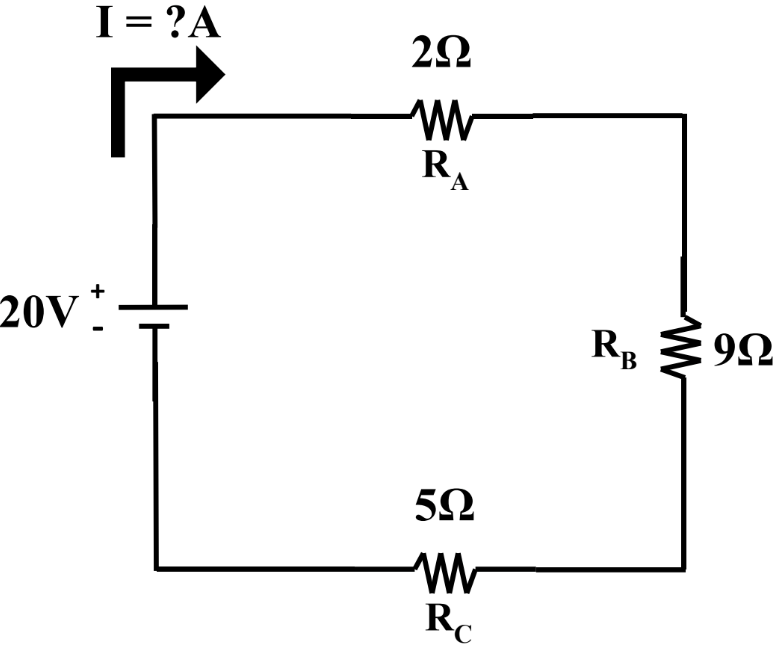
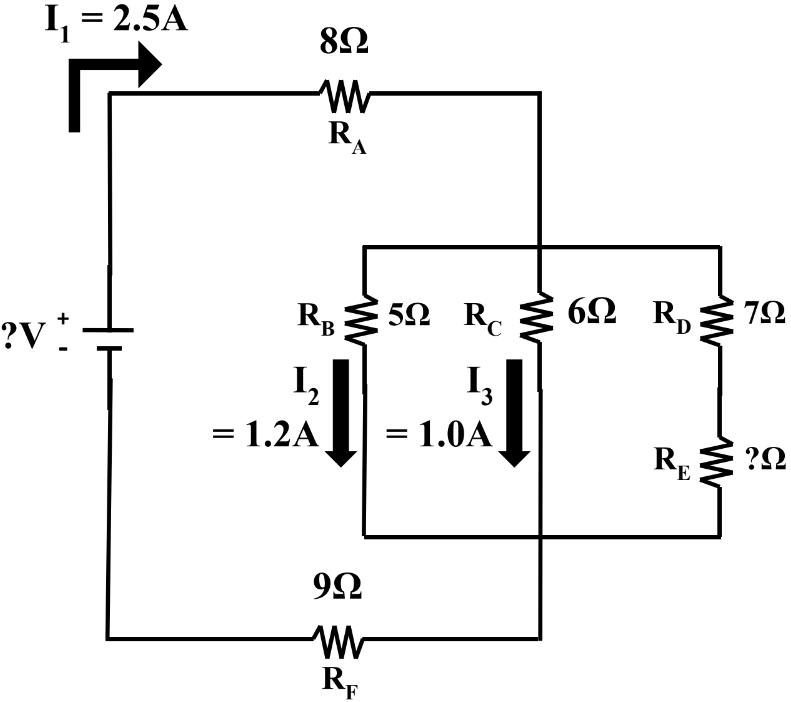
    • Voltage: Kirchhoffs 2nd Rule: Loop Rule (sum of all voltages around the loop equal zero); all parallel branches are equal to the same voltage drop
    • Current: Kirchhoffs 1st Rule: Junction Rule (sum of all currents into a junction equal to sum of all currents out of the junction) >
    • Resistance: total equivalent resistance in series ( Req(series)=∑k=1nRk R_{eq(series)} = \sum_{k=1}^{n} R_{k} ) and in parallel (Req(parallel)=1∑k=1n1Rk R_{eq(parallel)} =\frac{1} { \sum_{k=1}^{n} \frac{1}{R_{k}} } )
Concept

Introduction to Ohm's Law

Ohm's Law is a fundamental principle in electrical circuits that describes the relationship between voltage, current, and resistance. Named after German physicist Georg Ohm, this law is crucial for understanding how electricity flows through various components. Our introduction video provides a visual explanation of this concept. In electrical circuits, Ohm's Law helps engineers and technicians predict how changes in one variable will affect the others. This article will delve into the key components of Ohm's Law: voltage (the electrical pressure), current (the flow of electrons), and resistance (the opposition to current flow). We'll explore how these elements interact and influence each other in different circuit configurations. By mastering Ohm's Law, you'll gain a solid foundation for analyzing and designing electrical systems, from simple household wiring to complex electronic devices. Understanding this principle is essential for anyone working with or studying electrical circuits.

FAQs

  1. What is Ohm's Law and why is it important?

    Ohm's Law is a fundamental principle in electrical engineering that describes the relationship between voltage (V), current (I), and resistance (R) in an electrical circuit. It states that V = I × R. This law is crucial because it allows engineers and technicians to predict how changes in one variable will affect the others, enabling the design and analysis of electrical circuits.

  2. How can I apply Ohm's Law in practical situations?

    Ohm's Law can be applied in various practical situations, such as calculating the correct resistor value for an LED circuit, determining the current draw of a device, or sizing wires for electrical installations. For example, if you know the voltage of a power source and the desired current for a device, you can use Ohm's Law to calculate the required resistance: R = V / I.

  3. What are the limitations of Ohm's Law?

    While Ohm's Law is widely applicable, it has some limitations. It assumes a linear relationship between voltage and current, which doesn't hold true for all materials or components. It also assumes constant temperature, as resistance can change with temperature in some materials. Additionally, Ohm's Law is most directly applicable to DC circuits and may require modifications for AC circuits.

  4. How does Ohm's Law relate to power in electrical circuits?

    Ohm's Law is closely related to electrical power calculations. The power equation P = VI can be combined with Ohm's Law to derive additional formulas: P = I²R and P = V²/R. These relationships allow for the calculation of power consumption in circuits, which is crucial for designing efficient electrical systems and managing energy use.

  5. Can Ohm's Law be used in complex circuits with multiple components?

    Yes, Ohm's Law can be applied to complex circuits with multiple components. In series circuits, the total resistance is the sum of individual resistances, and the current is constant throughout. In parallel circuits, the voltage is constant across components, and the inverse of the total resistance is the sum of the inverses of individual resistances. By using these principles along with Ohm's Law, you can analyze and solve for unknown values in complex circuits.

Prerequisites

Before delving into the intricacies of Ohm's Law, it's crucial to have a solid foundation in certain fundamental concepts of electricity and physics. Two key prerequisite topics that are essential for a comprehensive understanding of Ohm's Law are electric potential and electric potential energy and the electric field.

Understanding electric potential difference is paramount when studying Ohm's Law. This concept forms the basis for comprehending voltage, which is a key component in the Ohm's Law equation. Electric potential difference, often simply referred to as voltage, represents the energy per unit charge available to move electrons in a circuit. It's the driving force behind the flow of electric current, which is central to Ohm's Law.

The concept of electric field is equally important in grasping Ohm's Law. An electric field is the region around a charged particle or object where its influence can be felt by other charged particles. This fundamental idea helps in visualizing how electric charges interact and move within a conductor, which is essential for understanding the flow of current in relation to Ohm's Law.

When you have a solid grasp of these prerequisite topics, you'll find that Ohm's Law becomes much more intuitive. For instance, knowing about electric potential difference allows you to better understand why increasing voltage leads to an increase in current, assuming resistance remains constant. Similarly, your knowledge of electric fields will help you visualize how charges move through a conductor and how this movement is affected by the material's resistance.

Moreover, these concepts provide a broader context for Ohm's Law. While Ohm's Law itself is a relatively simple equation (V = IR), its applications and implications become much clearer when you understand the underlying physics. For example, the relationship between electric field strength and current density in a conductor is directly related to Ohm's Law, but this connection is only apparent when you have a good foundation in both electric fields and Ohm's Law.

In conclusion, taking the time to thoroughly understand electric potential and electric potential energy as well as the electric field will greatly enhance your ability to work with Ohm's Law. These prerequisite topics provide the necessary context and foundational knowledge, allowing you to not just memorize the law, but truly comprehend its significance and applications in electrical systems and circuits.