Magnetic field due to a long straight wire & force between two parallel wires

In this lesson, we will learn:

• Magnetic field due to a long straight wire
• Magnetic field midway between two currents
• Forces between two parallel wires

Notes:

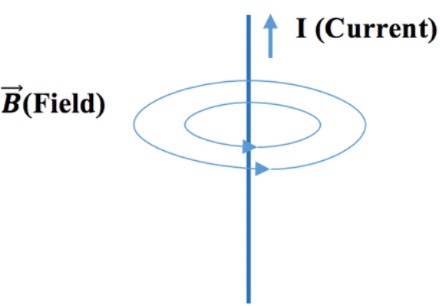
An electric current produces a magnetic field

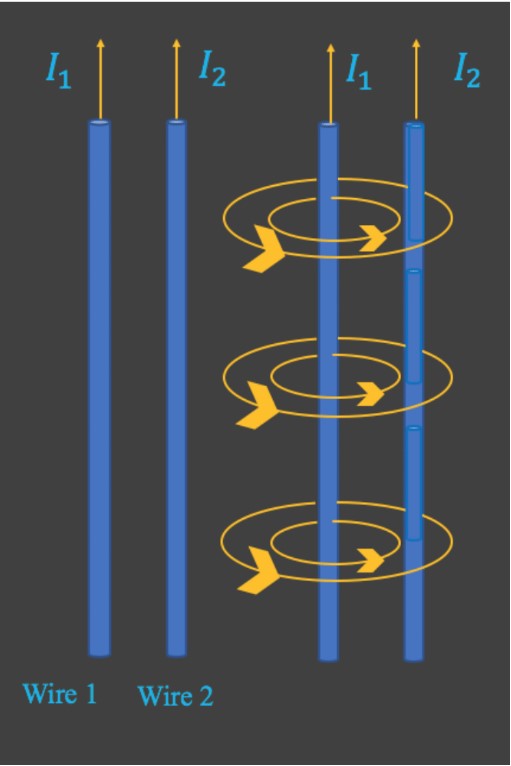
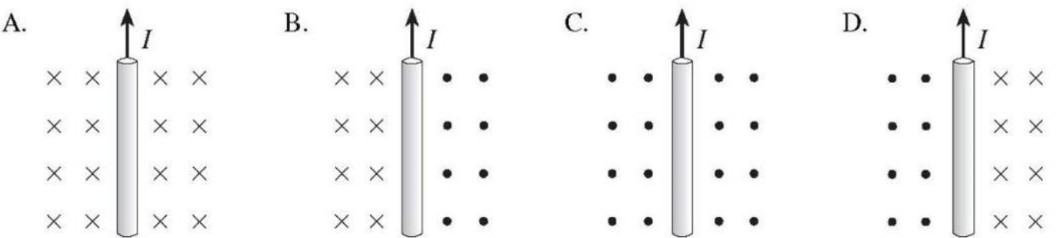
• The magnetic field surrounding the electric current in a long straight wire is such that the field lines are circles with the wire at the center.
• The field strength at a given point would be greater if the current flowing in the wire were greater; $B \propto I$
• The filed strength would be less at points farther from the wire $B \propto \frac{1}{r}$;


$\quad B \propto I$
$\quad B \propto \frac{1}{r} \qquad B \propto \frac{1}{r} \quad \Rightarrow \quad B =$ $\large \frac{\mu_{0}}{2 \pi} \frac{I}{r}$,

The value of the constant $\mu_{0}$, which is called the permeability of free space, is $\mu_{0}$ = 4$\pi$ × 10^-7 $T.m/A$



Magnetic Field Midway Between Two Currents
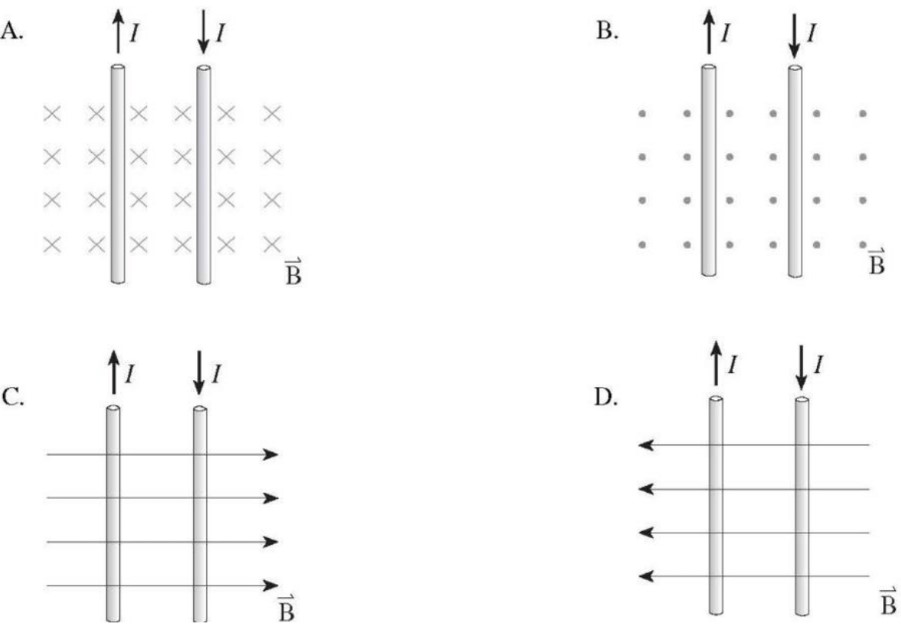
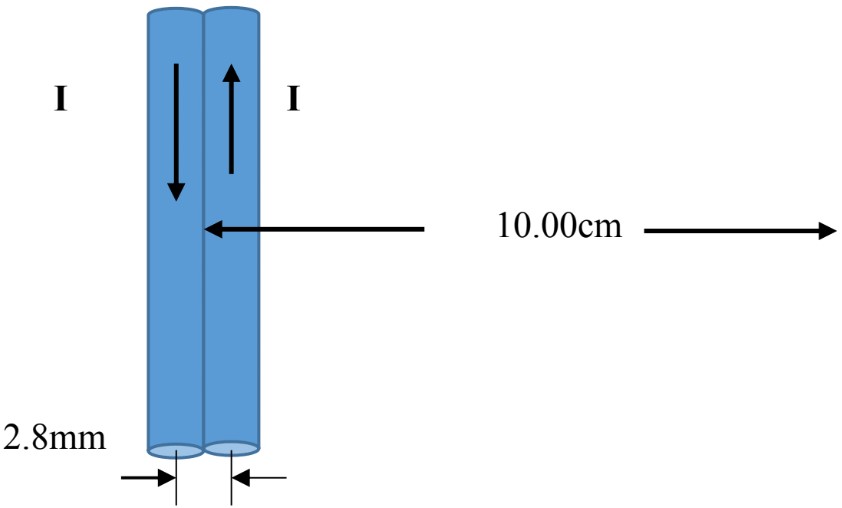
Two parallel wires 10.0cm apart carry currents in opposite directions. Current $I_{1}$ = 5.0A is out of the page, $I_{2}$=7.0 A is into the page. Determine the magnitude and direction of the magnetic field halfway between the two wires.



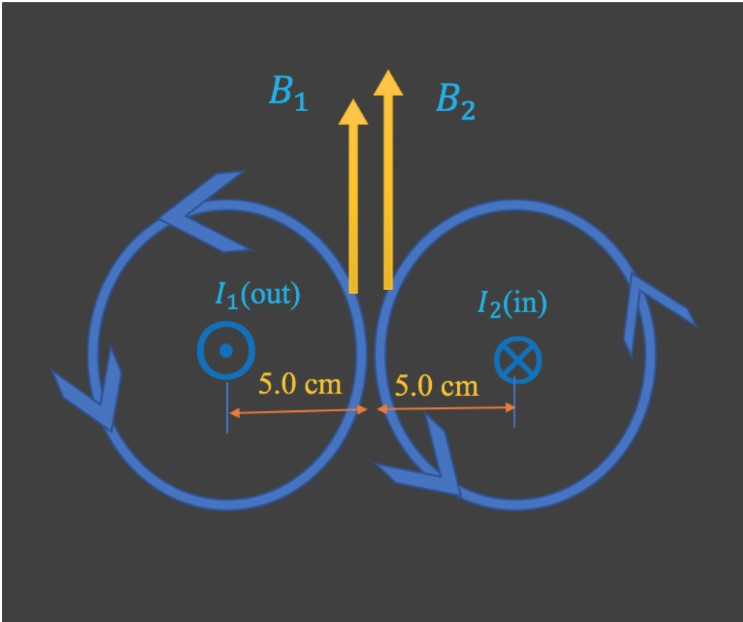
$B_{1} =$ $\large \frac{\mu_{0} I_{1}} {2\pi r} = \frac{(4\pi \, \times \, 10^{-7} \, T\, . \, m/A) (5. 0A) } {2 \pi (0.050m) }$ = 2.0 × 10^-5 $T$

$B_{2} =$ $\large \frac{\mu_{0} I_{2}} {2\pi r} = \frac{(4\pi \, \times \, 10^{-7} \, T\, . \, m/A) (7. 0A) } {2 \pi (0.050m) }$ = 2.8 × 10^-5 $T$

The total filed is up with the magnitude of

$B = B_{1} +B_{2} = 4.8 \times 10^{-5} T$


Forces Between Two Parallel Wires

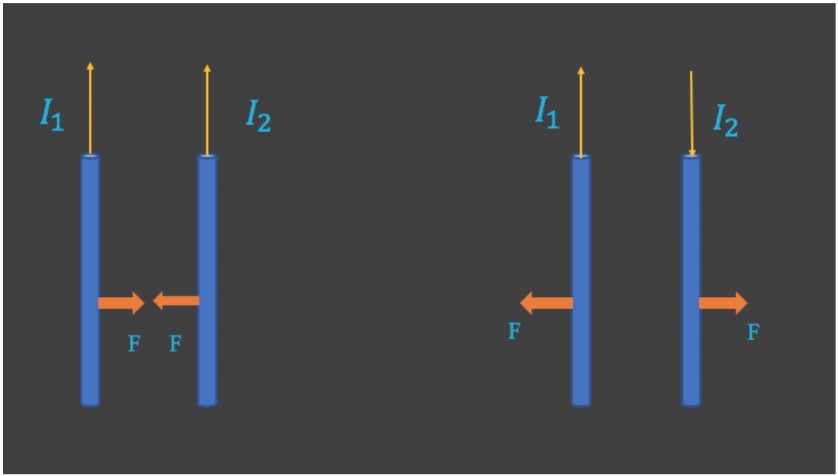
• Consider two long parallel wires separated by a distance $d$. They carry currents $I_{1}$ and $I_{2}$, respectively. Each current produces a magnetic field that is felt by the other, so each must exert a force on the other.





• Magnetic field $B_{1}$ produced by $I_{1}, \, B_{1} =$ $\large \frac{\mu_{0} I_{1}} {2 \pi d}$
• The force $F_{2}$ is exerted by $B_{1}$ on a length of $I_{2}$ of wire 2, carrying current $I_{2}$, $F_{2}$ = $I_{2}$ $B_{1}$ $I_{2}$
• Substitute $B_{1}$ into $F_{2}$ formula to get the final equation;


$F_{2} =$ $\large \frac{\mu_{0}} {2 \pi} \frac{I_{1} I_{2}} {d} I_{2}$

• Parallel currents in the same direction exert an attractive force on each other
• Antiparallel currents (in opposite directions) exert a repulsive force on each other.