Sign In
Try for Free
 flag-ca

Mastering Unequal Probability Outcomes in Mathematics
Dive into the world of unequal probability outcomes. Learn to calculate, interpret, and apply these concepts to real-life scenarios, enhancing your decision-making skills in various fields.

  1. Intros0/3 watched
  2. Examples0/6 watched
  3. Practice0% mastered
  1. 0/3
  2. 0/6
  3. 0%
Now Playing:Unequal probability outcomes – Example 0a
Intros
0/3 watched
  1. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
  2. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
    What is probability?
  3. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
    Even chances vs. not even chances
Examples
0/6 watched
  1. Outcomes are the result of flipping coins, rolling dice, or turning a spinner's arrow
    List all the possible outcomes. How many outcomes are there in total?
    1. A spinner with 5 parts with the colors red, blue, or yellow
      Unequal Probability Outcomes

    2. A bag of 7 marbles with the colors blue, yellow, green or orange
      Unequal Probability Outcomes

Practice
0%
Build your skill!Try your hand with these practice questions.
Sign Up
Unequal probability outcomes
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • In some probability scenarios, the outcomes are NOT all equally as likely to happen. Some outcomes will happen more often than others (have a greater chance of happening).
  • How to write a probability fraction for events that have unequal outcomes

Notes:

  • The outcomes for probability situation examples (coin toss, dice roll, equal parts spinner) have all had the same chance of happening. When all outcomes are just as likely (equally likely) to happen, there are even chances or equal chances of happening

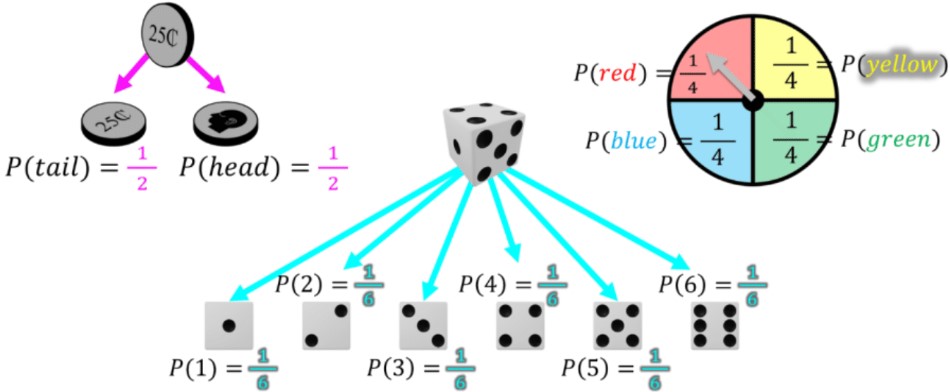
Unequal Probability Outcomes

    • When all outcomes are just as likely (equally likely) to happen, it is called having even chances
    • Probabilities can be compared across different situations. The outcomes of the coin are more likely than the spinner, which are more likely than the outcomes of the die (12\frac{1}{2} > 14\frac{1}{4} > 16\frac{1}{6} )

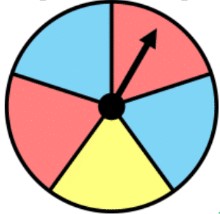
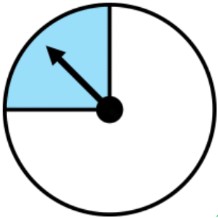
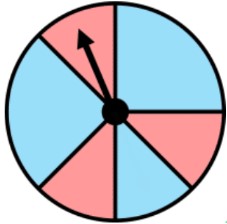
  • It is also possible for the outcomes to NOT be equally as likely; there are unequal chances of happening

Ex. unequal vs. equal outcomes for a spinner
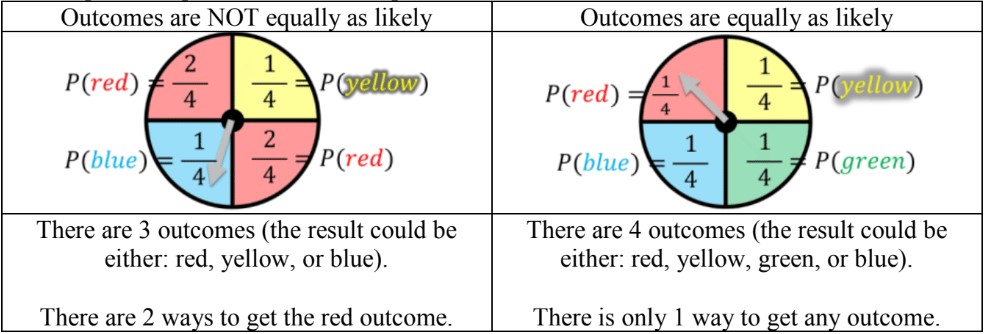
Unequal Probability Outcomes

  • The probability for situations with unequal outcomes can be given as a fraction in this formula format:

PP(event) = number ways to get the outcomenumber total ways of getting outcomes\frac{number\,ways\,to\,get\,the\,outcome}{number\,total\,ways\,of\,getting\,outcomes}
Concept

Introduction to Unequal Probability Outcomes

Unequal probability outcomes are a fundamental concept in probability theory. This lesson introduces the basics of probability math and how it differs from arithmetic math. The accompanying introduction video serves as a crucial starting point, providing a visual and interactive way to grasp these concepts. In probability, not all outcomes are equally likely to occur, which is where unequal probability comes into play. Unlike arithmetic math, where calculations are straightforward, probability math deals with uncertainty and varying likelihoods. Understanding unequal probability is essential for analyzing real-world scenarios, from weather forecasts to game strategies. This lesson will cover key principles, such as the probability distribution, expected value, and how to calculate probabilities when outcomes have different likelihoods. By mastering these concepts, you'll gain valuable insights into decision-making under uncertainty and develop a more nuanced understanding of chance events in various fields, including statistics, finance, and science.

FAQs

  1. What is the difference between even chances and unequal probability outcomes?

    Even chances occur when all possible outcomes have an equal likelihood of happening, such as flipping a fair coin where both heads and tails have a 50% chance. Unequal probability outcomes, on the other hand, involve scenarios where some results are more likely than others. For example, a weighted die might have a higher chance of landing on certain numbers.

  2. How do you calculate probabilities for unequal outcomes?

    To calculate probabilities for unequal outcomes, you need to consider the proportion of the total possibility that each outcome represents. For instance, if you have a spinner with unequal sections (40% red, 30% blue, 20% green, 10% yellow), the probability of landing on red would be 0.4 or 40%. The key is to divide the number of favorable outcomes by the total number of possible outcomes, taking into account their unequal weights.

  3. Can you provide an example of unequal probability in real life?

    A common real-life example of unequal probability is weather forecasting. The probability of rain on a given day might be 30%, while the probability of a clear day could be 70%. These unequal probabilities are based on various meteorological factors and historical data, reflecting that some weather outcomes are more likely than others in specific conditions.

  4. How does understanding unequal probability help in decision-making?

    Understanding unequal probability is crucial for making informed decisions in various fields. In finance, it helps in assessing investment risks and potential returns. In healthcare, it aids in identifying high-risk populations for diseases. In business, it can inform marketing strategies by predicting customer behavior. By recognizing that not all outcomes are equally likely, decision-makers can better evaluate risks and opportunities in complex scenarios.

  5. What are some common mistakes people make when dealing with unequal probability outcomes?

    One common mistake is assuming all outcomes are equally likely when they're not. Another is failing to consider all possible outcomes or misinterpreting probability data. People might also overlook the importance of sample size or ignore underlying factors that contribute to unequal probabilities. It's crucial to gather accurate data, consider all relevant factors, and apply proper statistical methods when analyzing unequal probability scenarios to avoid these pitfalls.

Prerequisites

Understanding unequal probability outcomes is a crucial concept in statistics and probability theory. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in basic probability concepts and mathematical reasoning is essential for grasping the intricacies of unequal probability outcomes.

Unequal probability outcomes refer to situations where different events or outcomes in a probability experiment have varying likelihoods of occurring. This concept is fundamental in many real-world applications, from analyzing survey data to making predictions in complex systems. To fully appreciate and work with unequal probability outcomes, students should have a solid understanding of basic probability principles, including the concept of sample spaces, events, and probability distributions.

Although not explicitly listed as prerequisites, topics such as basic probability theory, set theory, and elementary statistics provide a strong foundation for exploring unequal probability outcomes. Familiarity with these areas helps students grasp the underlying principles and mathematical frameworks used to analyze and interpret scenarios involving unequal probabilities.

Additionally, a good grasp of mathematical notation and algebraic manipulation is beneficial when working with probability formulas and calculations related to unequal probability outcomes. These skills enable students to express and manipulate probabilities effectively, which is crucial when dealing with complex scenarios or advanced applications.

While not a direct prerequisite, exposure to data analysis and statistical inference can provide valuable context for understanding the practical applications of unequal probability outcomes. These areas often involve working with real-world data sets where events or outcomes have different probabilities of occurrence, making the concept of unequal probability outcomes particularly relevant.

It's worth noting that critical thinking and problem-solving skills are also invaluable when studying unequal probability outcomes. The ability to analyze complex scenarios, identify relevant information, and apply appropriate probability concepts is crucial for success in this area of study.

As students delve into the topic of unequal probability outcomes, they may find it helpful to review or strengthen their understanding of these foundational concepts. By doing so, they'll be better equipped to tackle the complexities of unequal probability scenarios and apply this knowledge to real-world problems in various fields, such as economics, social sciences, and data science.

In conclusion, while there are no specific prerequisites listed for unequal probability outcomes, a strong background in basic probability, mathematics, and analytical thinking provides an excellent starting point for exploring this important concept. Students who take the time to reinforce these fundamental skills will find themselves well-prepared to understand and work with unequal probability outcomes in both academic and practical contexts.