Sign In
Try for Free
 flag-ca

Probability Outcomes: Coins, Dice, and Spinners Demystified
Dive into the world of probability with coins, dice, and spinners. Understand likely and unlikely events, master probability fractions, and apply concepts to real-life scenarios. Elevate your math prowess today!

  1. Intros0/2 watched
  2. Examples0/7 watched
  3. Practice0% mastered
  1. 0/2
  2. 0/7
  3. 0%
Now Playing:Probability outcomes for coins dice and spinners – Example 0a
Intros
0/2 watched
  1. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
  2. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
    What is probability?
  3. Introduction to Probability Outcomes for Coins, Dice, and Spinners:
    What are outcomes in probability?
    1. Outcomes for flipping a coin
    2. Outcomes for rolling a 6-sided die
    3. Outcomes for a spinner with different regions
Examples
0/7 watched
  1. Outcomes are the result of flipping coins, rolling dice, or turning a spinner's arrow
    List all the possible outcomes. How many outcomes are there in total?
    1. A coin with a happy face or sad face on its sides
      Probability Outcomes for Coins, Dice, and Spinners

    2. An 8-sided die
      Probability Outcomes for Coins, Dice, and Spinners

    3. Two friends having a race against each other
      Probability Outcomes for Coins, Dice, and Spinners

Practice
0%
Build your skill!Try your hand with these practice questions.
Sign Up
Probability outcomes for coins, dice, and spinners
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • What is probability in math?
  • How to write probability as a fraction
  • How to list all the outcomes for probability events (using coins, dice, and spinners)

Notes:

  • Probability is math for events that only sometimes happen. The chances of something happening can be likely or unlikely to happen.
    • Calculating probability is like predicting the future. We are trying to get a measure of the chances that something will happen.

  • Arithmetic math (all basic operations; adding, subtracting, multiplying, dividing numbers) is certain. In comparison, probability math is uncertain--but still predictable.


  • Probability can be given as a fraction, following the formula format:


    • Probability = number of outcomes wantedtotal number possible outcomes\frac{number\,of\, outcomes\, wanted} {total\,number\,possible\,outcomes}

  • Outcomes are all the possible endings that could happen for a situation.
    • Some simple probability situations that are often used in math problems include: tossing a coin, rolling a six-sided die, and spinning the arrow on a spinner.

  • Coins: Probability Outcomes for Coins, Dice, and Spinners
    • If you toss a coin, it will land on a flat side—either on heads or tails
    • So, there are 2 possible outcomes to a coin toss: heads or tails
    • The probability of landing on heads is PP(heads) = 12\frac{1}{2}
    • The probability of landing on heads is PP(tails) = 12\frac{1}{2}

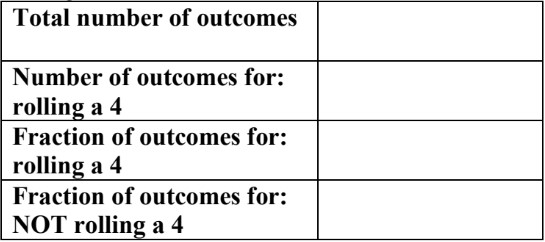
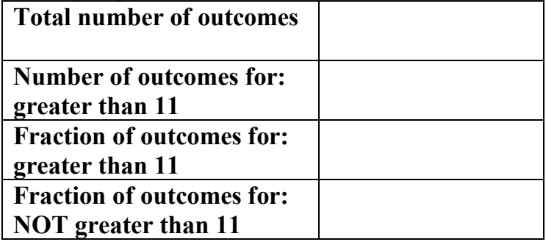
  • Dice: Probability Outcomes for Coins, Dice, and Spinners (a six-sided die, if singular)
    • When rolling a die, it will land with one of its six flat faces facing up (on top). There are six sides labelled from 1 to 6.
    • So, there are 6 possible outcomes to a die roll: 1, 2, 3, 4, 5, or 6
    • The probability of landing on any one side (1-6) is one out of six chances
    • PP (1) =PP (2) = PP (3) = PP (4) = PP (5) = PP (6) = 16\frac{1}{6}

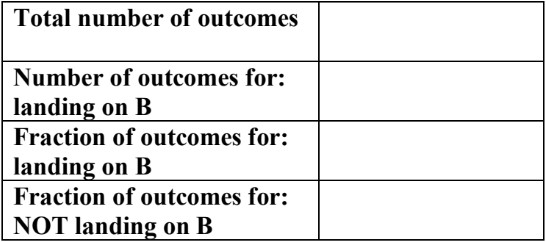
  • Spinners: 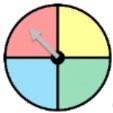Probability Outcomes for Coins, Dice, and Spinners (can have any number of equal parts; labels with numbers, letters, etc.)
    • When using a spinner, the arrow will land on one of the marked regions. In this case, there are 4 different coloured regions.
    • So, there are 4 possible outcomes for this spinner: red, yellow, green, or blue
    • The probability of landing on any one of the colors is one out of four chances
    • PP (Red) = PP (Yellow) = PP (Green) = PP (Blue) = 14\frac{1}{4}
Concept

Introduction to Probability Outcomes

Welcome to the fascinating world of probability! Our introduction video sets the stage for understanding this essential mathematical concept. Probability is a branch of mathematics that deals with events that may or may not occur, making it both intriguing and practical. When we talk about probability, we often explore outcomes related to common objects like coins, dice, and spinners. These simple items help us grasp the fundamental ideas of likely and unlikely events. For instance, when flipping a coin, there are two possible outcomes: heads or tails. With dice, we have six potential results, while spinners can have various numbers of outcomes depending on their design. By studying these examples, we begin to understand how probability applies to real-world situations. Whether an event is likely or unlikely depends on the number of favorable outcomes compared to the total possible outcomes. This introduction lays the groundwork for deeper exploration into the world of probability and its wide-ranging applications in science, finance, and everyday decision-making.

FAQs

  1. What is the probability of getting heads when flipping a coin?

    The probability of getting heads when flipping a fair coin is 1/2 or 50%. This is because a coin has two equally likely outcomes (heads and tails), and there is one favorable outcome (heads) out of the two possible outcomes.

  2. How do you calculate the probability of rolling a specific number on a six-sided die?

    The probability of rolling any specific number on a standard six-sided die is 1/6 or approximately 16.67%. This is calculated by dividing the number of favorable outcomes (1, as there's only one face with the desired number) by the total number of possible outcomes (6, as there are six faces on the die).

  3. How does the number of sections on a spinner affect the probability of landing on a specific color?

    The number of sections on a spinner directly affects the probability of landing on a specific color. If all sections are equal in size, the probability is calculated by dividing 1 by the total number of sections. For example, on a spinner with 4 equal sections, the probability of landing on any specific color is 1/4 or 25%. If the sections are unequal, the probability is proportional to the size of each section relative to the whole spinner.

  4. What is the difference between theoretical and experimental probability?

    Theoretical probability is the expected probability based on the number of possible outcomes, calculated mathematically. For example, the theoretical probability of rolling a 3 on a six-sided die is 1/6. Experimental probability is based on the actual results of repeated trials. While experimental probability should approach theoretical probability over a large number of trials, it may vary in smaller sample sizes due to random chance.

  5. How can understanding probability in coins, dice, and spinners help in real-world situations?

    Understanding probability through these simple objects provides a foundation for analyzing more complex real-world scenarios. It helps in decision-making under uncertainty, risk assessment, and strategic planning. For example, this knowledge can be applied in fields like weather forecasting (predicting the likelihood of rain), finance (assessing investment risks), or even in everyday decisions like choosing the best route to avoid traffic based on probabilities of congestion.

Prerequisites

Understanding probability outcomes for coins, dice, and spinners is a fundamental concept in mathematics and statistics. While this topic doesn't have specific prerequisites listed, it's important to recognize that a strong foundation in basic mathematical concepts is crucial for grasping these probability concepts effectively.

To fully comprehend probability outcomes for coins, dice, and spinners, students should have a solid understanding of fractions, decimals, and percentages. These mathematical tools are essential for expressing probabilities accurately. For instance, when calculating the probability of rolling a specific number on a die, you'll need to express it as a fraction (e.g., 1/6) or convert it to a decimal or percentage.

Additionally, a basic understanding of set theory can be beneficial. While not explicitly required, familiarity with sets and subsets can help in visualizing and organizing possible outcomes in probability scenarios. This knowledge aids in identifying favorable outcomes and the total number of possible outcomes, which are crucial components in probability calculations.

Basic arithmetic skills are also important prerequisites. Students should be comfortable with addition, subtraction, multiplication, and division, as these operations are frequently used in probability calculations. For example, when determining the probability of multiple events occurring together, multiplication of individual probabilities is often necessary.

Furthermore, an introduction to basic statistical concepts can provide valuable context. While not strictly required, understanding concepts like randomness and sample space can enhance a student's grasp of probability outcomes. These ideas help in conceptualizing the nature of chance events and the range of possible results.

Logical reasoning skills are another implicit prerequisite. The ability to think critically and analyze different scenarios is crucial when working with probability. Students need to be able to identify all possible outcomes and understand how different events relate to each other.

Lastly, familiarity with graphical representations can be helpful. While not a strict prerequisite, the ability to interpret and create simple graphs and charts can aid in visualizing probability distributions, especially when dealing with spinners or more complex probability scenarios.

By ensuring a strong foundation in these fundamental mathematical and logical concepts, students will be better equipped to tackle the intricacies of probability outcomes for coins, dice, and spinners. This solid base allows for a smoother transition into more advanced probability topics and applications in various fields, from statistics to data science and beyond.