In this lesson, we will learn:
- Compound probability is for finding the chances of an event involving two simple probability scenarios
- How to draw a probability tree to show all possible outcomes for a compound event
- How to use an outcome table to show all possible outcomes for a compound event
- How to calculate compound probability fractions
Notes:
- Compound probability (or probability for compound events) is the chances of an event—involving two probability scenarios—happening.
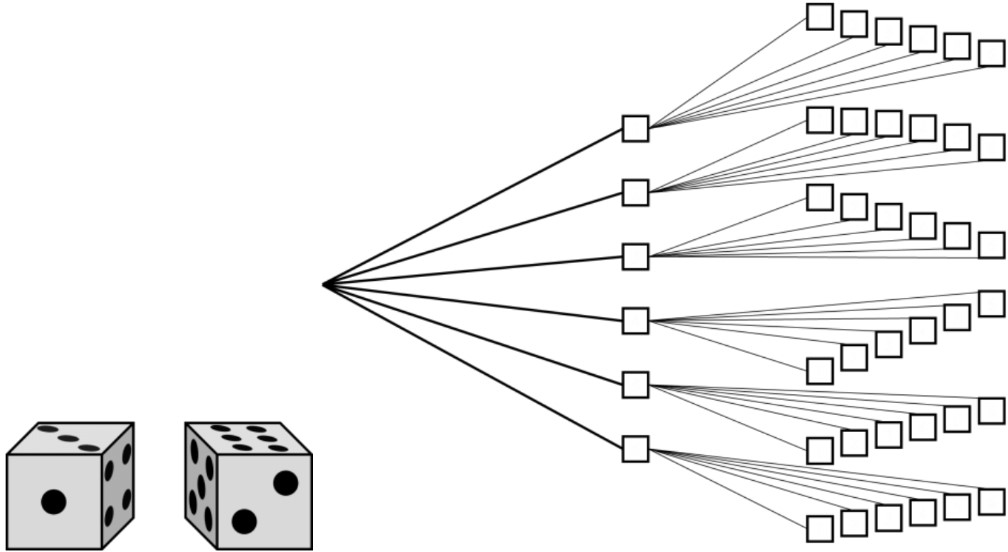
- Some examples of compound situations: flipping 2 coins, rolling 2 dice, spinning the arrow on 2 spinners, or (combinations like) a coin flip and a die roll.
- Showing all possible outcomes for compound events will be different than probability for simple events. A probability tree or outcome table can be used
- A probability tree can be drawn vertically or horizontally. Each level represents each simple event: start at a point and draw branches for all possible outcomes. At the next level, the end of each previous branch will be a new starting point. Draw branches for all possible outcomes for the second simple event.
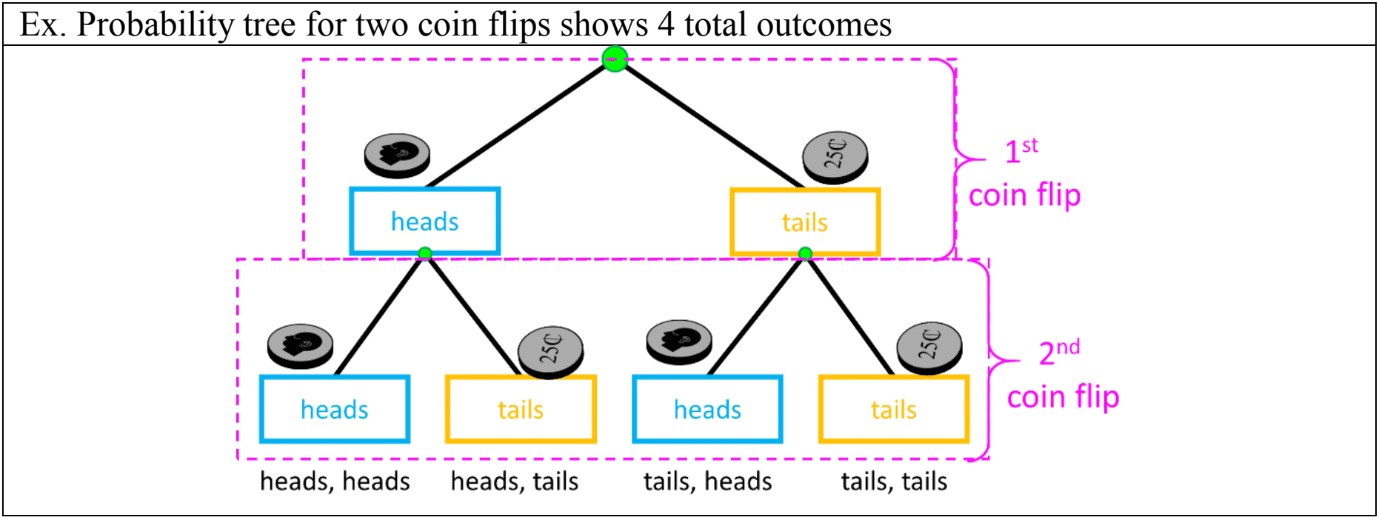
- Another way to find all outcomes for compound events is by using an outcome table, crossing all outcomes for the first event in the rows, by all the outcomes for the second outcomes in the columns.
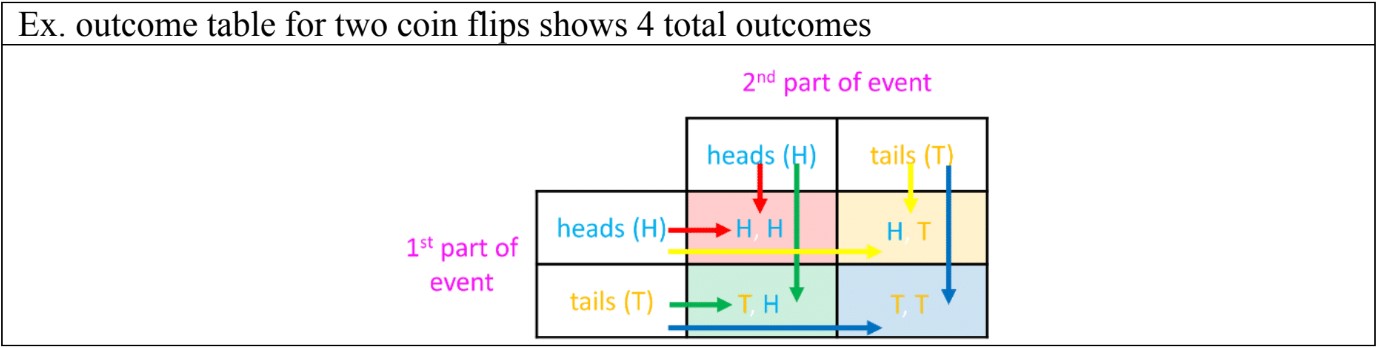
- The total number of outcomes can be calculated:
total outcomes = (#outcomes 1st event) × (#outcomes 2nd event) - The formula (event) = can also be used for compound probability
- Or, using fraction multiplication, compound probability for an event can also be found using the formula:
Compound Probability = (1st event) × (2nd event)