Sign In
Try for Free
 flag-ca

Understanding Likelihood for Simple Events: A Probability Guide
Dive into the world of probability with our comprehensive guide on likelihood for simple events. Learn to calculate, visualize, and apply probability concepts to real-world scenarios.

  1. Intros0/3 watched
  2. Examples0/9 watched
  3. Practice0% mastered
  1. 0/3
  2. 0/9
  3. 0%
Now Playing:Likelihood for simple events – Example 0a
Intros
0/3 watched
  1. Introduction to Basic Probability for Simple Events:
  2. Introduction to Basic Probability for Simple Events:
    How to describe the likelihood of something happening
  3. Introduction to Basic Probability for Simple Events:
    Likelihood on a probability number line
Examples
0/9 watched
  1. Expectation and likelihood for simple events
    Draw a point on the probability line for the likelihood of the event to happen. Describe using one of the words: likely, unlikely, impossible, certain, or equally likely.
    Likelihood for Simple Events
    1. Rolling greater than 3 on a six-sided die

    2. Rolling less than 7 on a six-sided die

    3. Rolling the number 6 on a six-sided die

    4. Rolling the number 8 on a six-sided die

    5. Rolling greater than 2 on a six-sided die

Practice
0%
Build your skill!Try your hand with these practice questions.
Sign Up
Likelihood for simple events
Jump to:NotesConceptFAQsPrerequisites
Notes

In this lesson, we will learn:

  • What is the likelihood of different probability events?
  • The likelihood of an event can either be: impossible, unlikely, as likely as not, likely, or certain
  • How to understand likelihood using a probability line (probability number line)

Notes:

  • The probability of an event is a value of how likely it is to happen. We can quantify the chances of something happening using a probability fraction: PP(event) = number outcomes wantedtotal number possibilities\frac{number\,outcomes\,wanted}{total\,number\,possibilities}

  • The likelihood of an event can be described using the following phrases:
    • Impossible - it will never happen
    • Unlikely - low chances of happening (less than half the chances)
    • As likely as not - just as likely to happen as to not happen (even chances; exactly half the chances)
    • Likely - high chances of happening (more than half the chances)
    • Certain - it will always happen (happen for sure)

  • How does the value of the probability fraction represent the likelihood of an event?
    • It can tell us how likely or unlikely something is to happen.
    • The tool we can use to help us understand likelihood is the probability number line (probability line)
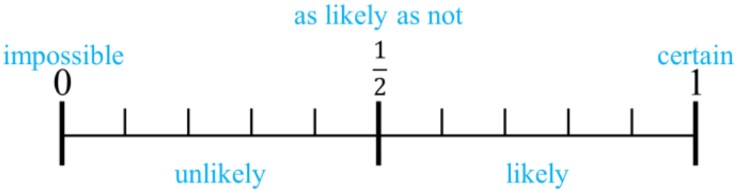
Likelihood for Simple Events

  • The probability line goes from 0 to 1 because the smallest probability fraction for any event is 0 out of any number of outcomes. The greatest probability fraction for any event is that it always happens (100% of the time = fraction of 1 whole).

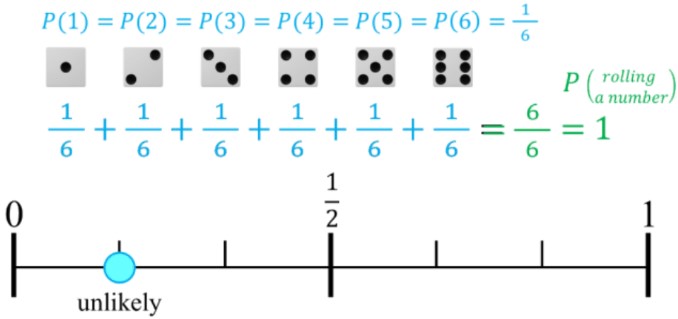
  • Ex. For rolling a six-sided die, there is a 1 in 6 chance to land on any numbered side. Rolling any of the six numbers has a low chance (all the outcomes are unlikely events).
    • If you add all the probability fractions of all outcomes, the answer will be 1 whole (considering every single possible result)
Likelihood for Simple Events
Concept

Introduction to Likelihood for Simple Events

Welcome to our exploration of likelihood for simple events, a fundamental concept in probability theory. Our journey begins with an engaging introduction video that lays the groundwork for understanding probability. This visual presentation is crucial in grasping the core principles of likelihood. As we delve deeper, we'll uncover the intricacies of probability fractions, providing you with the tools to quantify the chances of various outcomes. We'll also introduce the probability number line, a visual aid that helps in comparing and contrasting different likelihoods. Throughout this lesson, we'll examine various types of likelihoods, from certain events to impossible ones, and everything in between. By the end of this section, you'll have a solid foundation in probability concepts, enabling you to analyze simple events with confidence. Whether you're a student or a professional, mastering these basics is essential for tackling more complex probability problems in the future.

FAQs

  1. What is the difference between probability and likelihood?

    While often used interchangeably, probability and likelihood have distinct meanings in statistics. Probability refers to the chance of an event occurring and is calculated based on the number of favorable outcomes divided by the total number of possible outcomes. Likelihood, on the other hand, is a function that describes how well a statistical model fits observed data. In simple terms, probability is used to predict future events, while likelihood is used to evaluate how well a model explains observed data.

  2. How do you calculate the probability of mutually exclusive events?

    For mutually exclusive events (events that cannot occur simultaneously), the probability of either event occurring is the sum of their individual probabilities. For example, if the probability of rolling a 1 on a die is 1/6, and the probability of rolling a 2 is also 1/6, then the probability of rolling either a 1 or a 2 is 1/6 + 1/6 = 1/3.

  3. What is the law of large numbers in probability theory?

    The law of large numbers states that as the number of trials of a random process increases, the average of the results gets closer to the expected value. For instance, if you flip a fair coin many times, the proportion of heads will approach 50% as the number of flips increases. This law is fundamental in understanding how probability works in real-world applications and why larger sample sizes generally lead to more accurate predictions.

  4. How does conditional probability differ from independent probability?

    Conditional probability is the probability of an event occurring given that another event has already occurred. It's calculated using the formula P(A|B) = P(A and B) / P(B). Independent probability, conversely, means that the occurrence of one event does not affect the probability of another event. For independent events, P(A and B) = P(A) * P(B). Understanding the difference is crucial in many real-world scenarios where events may or may not influence each other.

  5. What is the importance of understanding probability in everyday life?

    Understanding probability is crucial in everyday life as it helps in making informed decisions under uncertainty. It's used in weather forecasting, financial planning, risk assessment, and even in understanding health risks. For example, knowing the probability of rain helps you decide whether to carry an umbrella, while understanding the odds in games of chance can help you make better gambling decisions. In broader terms, probability literacy enables critical thinking about statistics presented in news and research, helping to interpret information more accurately in various aspects of life.

Prerequisites

Understanding the concept of likelihood for simple events is a fundamental aspect of probability theory and statistics. While this topic doesn't have any specific prerequisites listed, it's important to recognize that a strong foundation in basic mathematical concepts can greatly enhance your comprehension of likelihood and probability.

Likelihood for simple events is a concept that builds upon our intuitive understanding of chance and uncertainty. It quantifies the probability of a specific outcome occurring in a given scenario. To fully grasp this concept, students should be comfortable with basic arithmetic, fractions, and percentages, as these mathematical tools are often used to express and calculate probabilities.

Although not explicitly listed as prerequisites, familiarity with set theory and basic logic can be beneficial when studying likelihood. These concepts help in understanding how different events relate to each other and how to reason about probabilities in various situations. Additionally, a basic understanding of data representation and analysis can provide context for applying likelihood concepts in real-world scenarios.

While exploring likelihood for simple events, students will encounter terms such as "sample space," "favorable outcomes," and "equally likely events." These concepts form the building blocks for more advanced probability topics. Having a solid grasp of these foundational ideas will make it easier to progress to more complex probability concepts in the future.

It's worth noting that likelihood for simple events is often an entry point into the broader field of probability theory. As such, it serves as a prerequisite for more advanced topics like conditional probability, Bayes' theorem, and probability distributions. Mastering this concept will pave the way for a deeper understanding of statistical inference and data analysis techniques.

In practical applications, likelihood for simple events is used in various fields, including science, engineering, finance, and decision-making processes. Understanding this concept can help in assessing risks, making predictions, and interpreting data-driven results. This wide applicability underscores the importance of building a strong foundation in the basics of probability.

As students delve into the study of likelihood for simple events, they should approach the topic with curiosity and an open mind. Engaging with practical examples and real-world applications can help reinforce the theoretical concepts and demonstrate their relevance in everyday situations. By doing so, students will not only gain proficiency in calculating probabilities but also develop critical thinking skills that are valuable across many disciplines.

In conclusion, while there are no specific prerequisites listed for likelihood for simple events, a strong mathematical foundation and an understanding of basic logical reasoning will greatly benefit students approaching this topic. As they progress in their studies, the concepts learned here will serve as crucial building blocks for more advanced probability and statistics courses, making it an essential topic in the mathematical curriculum.