Sampling methods
0/1
Intros
Lessons
- Importance of knowing the nature of the purpose and the population of your study
Sampling Methods
a) Simple Random:
• Each subject is chosen by chance and all subjects have equal likelihood of being chosen.
• All sub-groups have equal probability of being chosen.
b) Stratified:
• The population is divided into groups (called stratas) based off characteristics, and then random subjects are chosen from each strata.
c) Convenience:
• A non-random sample.
• Formed by subjects who are easy to reach (convenient to reach).
d) Cluster:
• The population is first divided into randomly chosen sub-groups (called clusters), then a random assortment of these clusters are chosen to be the sample.
e) Systematic:
• The population is first formed into an exhaustive list, and then every member is chosen to be part of the sample.
0/5
Examples
Lessons
- Observations VS. Experiments
Determine if an observation or experiment should be used for the following situations.
i) A department store wants to know the most common route taken by its customers within the store.
ii) A researcher wants to find out if students will get a better grade if they chew on gums during an exam.
iii) A teacher wants to find out if children behave more aggressively towards each other the day after Halloween.
iv) A company wants to know if a lighter wall colour will improve the performance of its employees.
i) What are they?
ii) What are their advantages and disadvantages? - Two studies were done to find out if the time of a statistics class has an effect on the retention of class material in students. There are two classes: one in the morning and another one in the evening. In study A, 25 students were randomly assigned to the morning class while the other 25 were randomly assigned to the evening class. In study B, 25 students were randomly chosen from the morning class while the other 25 were randomly chosen from the evening class. Then, in both studies, all 50 students from both classes were given a test on the class material at the end of the class.
Which of the following statement(s) is/are true?
i) Both studies were observational studies.
ii) Both studies were experiments.
iii) Study B was an experiment because it had a control group.
iv) Study A was an experiment because it had a control group and a treatment group. - Sampling Methods
Define.
i) simple random sampling
ii) stratified sampling
iii) cluster sampling
iv) systematic sampling
v) convenience sampling - What kind of sampling technique was in each situation below (simple random, stratified, convenience, cluster, or systematic)?
i) 55 residents living in an apartment building were selected randomly and interviewed about their satisfaction towards the strata company.
ii)A study done by a university student council found that male students who major in Computer Science are 3 times more likely to have an experience staying overnight in the campus than other male students in other majors.
iii) The school board of City A wants to review the current Math curriculum. Therefore, 11 schools in the city were selected randomly and all Math teachers of these schools were asked to fill out a questionnaire on the subject matter.
iv) In a grocery store, every 70th receipt printed out from a cash register will ask the customers to do a survey on their shopping experience in exchange for a coupon.
v) Derek says, "ABC brand is the most popular cellphone brand in my school. I have asked the first 60 students who went to school today."
- Ivan is a Business student and he is doing a project on where college students usually shop online. He wants to have a simple random sample of 40 college students. Therefore, Ivan randomly interviewed 10 students from each year (first, second, third, and fourth year).
i) Did this sampling method allow Ivan to collect a random sample of 40 college students?
ii) Explain your answer in the previous part. If your answer is no, name the sampling method that was used by Ivan.
iii) What kind of data has Ivan collected?
Topic Notes
Glossary terms:
- Population
- Sample
- Sampling methods
- Simple random
- Stratified sampling
- Convenience sampling
- Cluster random sample
- Systematic
Sampling Methods
During our first lesson for this statistics course where we talked about classification of data, we learnt how statistics is a branch of mathematics in charge of gathering data in order to make conjectures based on the information collected.
Through that same lesson we learnt about the data types and how to use them; therefore, now that you know the kind of information that can be obtained through statistical research, it is time we learn about data sets, or, the collections of statistical variables that will be gathered for analysis.
First it is important you learn that there exist two types of data sets: populations and samples.
A statistical population is the set of all the outcomes, items, counts, measurements or responses which are of interest in an experiment or survey. Notice that a population of interest can be an infinite collection which is hypothetical, or it can be an existing physical group of items, this depends on the subject of the statistical study that it is being performed. For example, if we want to obtain statistical information about the people from different countries; when picking a specific country, the statistical population will be the population of the country itself. Such statistical population exists and could be counted one by one (even if that would take a large amount of time); on the contrary, when rolling a die we know the possible outcomes are six but they are hypothetical until they actually happen.
And so, what is a sample in statistics? A sample is a subset of a population; a smaller group selected from the population to represent it in order to obtain information of it. The action of obtaining a sample from a population is what we call sampling.
The usage of sampling methods in statistical research is imperative given that most large populations of interest cannot be surveyed in its entirety; therefore, a selection of subjects as diverse as the population it comes from, and which adds up to a much smaller group, can be used as a representative sample in order to infer information from the whole.
Let us take a look to an example of sample in statistics: If we wanted to find the average height of all the students in your school, if you happen to attend a school with a large population it would be difficult to conduct an operation where you would measure every single students height in the school. On the other hand, you could take a sample of the whole population by picking a group of 50 students who you would measure (simpler than measuring hundreds, or even thousands, of people). This 50 student sample will allow you to have an idea of what to expect for the information of the whole school.
On this same example, if you wanted to undertake the task of measuring every single students height from your school you would be working on a census, we will talk more about this concept in our next lesson on census and bias.
Sample population or population sampling? The usage of terms in statistics can get confusing, but dont worry, with time and practice you will be an accomplished statistician!
For a simple and quick clarification, remember that a sample population is the population of a sample, in other words, the items inside the sample (or the items that populate the sample); while population sampling refers to the action of obtaining a sample group from a population of interest.
Having learnt the sampling definition, and its origins from a population, we pass into our next section where we will explain the different types of sampling methods that can be used in statistical research.
Types of sampling methods
Remember that a sample of subjects for a statistical study will be the group of subjects you end up directly observing, interviewing, or experimenting on (be it inanimate objects or living organisms). Thus, in order to be able to generalize the study findings to a larger population, we need to be careful in the way we pick a representative sample of it; the sample itself needs to be fairly equivalent to the whole population, meaning that the same variables are found in the same proportion as in the general population of interest.
Since there are many variables to take into account when performing sampling techniques, and it all depends on the type of study or research you are trying to perform, there are a wide variety of statistical sampling methods that can be used while performing statistical research.
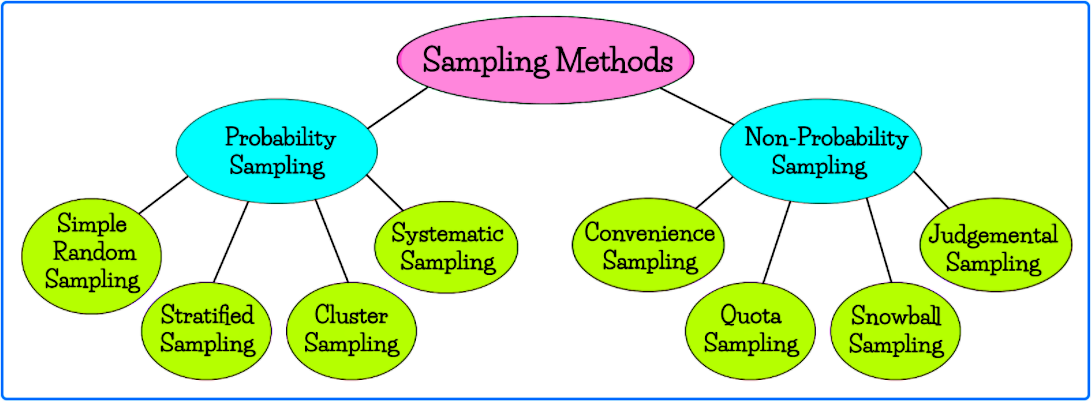
Notice that there are probability and non-probability sampling methods.
Probability sampling is based on the principle that all of the subjects in a population have the same chance of being part of the selected sample to study and analyse; meanwhile, in non-probability sampling, subjects in a population do not have the same probability to be part of the study, therefore, the samples obtained cannot be defined as representative of the whole population.
On this lesson we will mainly focus on probability sampling methods. Given that non-probability sampling leaves us with errors from the start, making any mathematical calculation with such data will produce results that are not representative of the population in question.
Let us take a look at the methods presented on the next list:
• Simple random
• Stratified sampling
During stratified random sampling the population is divided due to a particular characteristic of interest separating the population into groups called strata (giving the name to the technique); however, it is important to note that the population is not necessarily divided into groups with the same amount of subjects, and each subject is present in only one strata. After the division of the population into homogeneous groups, random sampling is done on each strata, and the size of the sample for each group must reflect the proportion of each particular strata in the population.
For example, let us say we want to find out how much of the adult population in your city drinks coffee right after they woke up each morning. In order to obtain a higher degree of information than just getting a random selection of 1000 adult people from the city, you could divide the adult population in the next three groups: recent graduates entering the workforce, people with 5 or more years on their profession, and retirees.
After separating the three strata mentioned above you find out that from 5 million people in your city, 2 million are recent graduates, 1.5 million have been in the workforce more than 5 years and 1.5 million have retired; therefore, now you can take a random sample from each of the stratas in proportion to their size: if your total sample size is 1000 people, you will obtain a sample of 400 random recent graduates, 300 random workers with more than 5 years on the job, and 300 random retirees. Such sampling method allows us to not only obtain more specific information for each group in the population, but a lower degree of error in estimates for further studies.
• Cluster random sample
Cluster sampling is usually useful when studying large populations spread around through a specific geographic area, thus producing geographic groupings (the clusters) that contain members with all the characteristics taken into consideration on the study; then, one or more of the clusters (not all) are selected to be used for the total sample in the statistical study.
Do not confuse cluster sampling with stratified sampling. In stratified sampling you divide the population into groups where each member shares a particular characteristic with the others in the group; meanwhile, in cluster sampling the groups have subjects with mixed characteristics and they have been separated mostly because of their location. Furthermore, the final sample for the statistical study obtained from stratified sampling comes from taking a sample of each of the strata, while the final sampling for a study using cluster sampling is at least one complete cluster from the bunch. Due to these characteristics, one must be very careful when using cluster sampling to always check that the clusters have similar characteristics; otherwise, the final sample for the study could not be representative of the population if it contains a cluster with a highly predominant characteristic in comparison with the others.
• Systematic sampling
In other words, in the systematic sampling method, a random periodic interval is chosen to start selecting subjects of the population from a starting point onwards; hence, this method can be thought as assigning a particular number to each subject in the population and order them based on this number, then, the starting point is randomly selected and sample members are picked at a regular interval after that starting point, making the whole affair very systemic-like (thus the name).
• Convenience sampling
The only thing required for a subject to participate in a study performing convenience sampling is to be available at the time of the study and to be willing to participate in it; hence, this sample selection process can be called availability sampling.
Whenever a survey is sent to you after you have purchased or received a service from a company, if you respond it and send back your feedback, you are becoming a part of the convenience sample for the companys commercial statistical analysis. ***Remember, from the five types of sampling presented in here, only convenience sampling is a non-probability sampling method.
Having learnt about the five sampling methods in statistics that we will cover on this lesson, we will be looking at examples of each of them on the next section. So get ready to gain some practice on identifying between the sampling strategies that could be out there in statistical research.
Sampling techniques examples
On this section, we will focus on identifying sampling methods in research for different areas of statistical analysis. It is important you pay attention to the target population in each case, so you can find out which of the types of sampling in statistics is being used:Example 1
From the types of sampling methods described above, what kind of technique was used in each situation below?1. 55 residents living in an apartment building were selected randomly and interviewed about their satisfaction towards the strata company.
Answer: Simple random sampling
On this example, a simple random group of 55 people were interviewed from the whole apartment building population. There was no other mechanism used in the survey, therefore, this is a typical simple random sampling example.
2. A study done by a university student council found that male students who major in Computer Science are 3 times more likely to have an experience staying overnight in the campus than other male students in other majors.
Answer: Stratified sampling
For this study, the campus male student population was divided in groups that shared a specific characteristic: their major. Therefore, this looks like stratified sampling at work.
3. The school board of City A wants to review the current Math curriculum. Therefore, 11 schools in the city were selected randomly and all Math teachers of these schools were asked to fill out a questionnaire on the subject matter.
Answer: Cluster random sampling
The entire school district of City A looked at its population by clusters, each cluster being a particular school from the district. Then the final sample to be studied was selected to be an amount of entire clusters from the population selected randomly; therefore, this reviews method is a cluster sampling example.
4. In a grocery store, every 70th receipt printed out from a cash register will ask the customers to do a survey on their shopping experience in exchange for a coupon.
Answer: Systematic sampling
The selection of the people to do the survey is done through a regular interval; thus, this is a systematic random sampling example.
5. Derek says, ABC brand is the most popular cell phone brand in my school. I have asked the first 60 students who went to school today.
Answer: Convenience sampling
Derek asked the first 60 students who were available for his survey at school that day, therefore, Dereks method is a convenience sampling example.
Example 2
Ivan is a Business student and he is doing a project on where college students usually shop online. He wants to have a simple random sample of 40 college students. Therefore, Ivan randomly interviewed 10 students from each year (first, second, third, and fourth year). Next we present to you three questions about Ivans case, please read them and answer them on your own before looking at their answers below:- Did this sampling method allow Ivan to collect a random sample of 40 college students?
- Explain your answer in the previous part. If your answer is no, name the sampling method that was used by Ivan.
- What kind of data has Ivan collected?
Ready with your answers? Here are ours to compare:
- Answer: NO
- Answer: Stratified sampling.
Ivan didnt just collect information from 40 random people from his college, he divided the student population in 4 groups where each group had a common characteristic: the same college year. Then he took a random sample from each group, thus completing the process of stratified sampling. - Answer: Qualitative data
To finalize this lesson, we recommend you to visit the next page on types of sampling where you can expand your knowledge on the non-probability sampling methods such as judgement sampling and how to get a voluntary response sample. Continuing with the topic of types of samples , this particular article shows you the other classification of samples: representative and non-representative, which are equivalent to the probability and non-probability division we have presented here. And finally, this little page on sampling methods quickly describes the two categories mentioned for sampling, including a few different names received for each method.
This is it for our lesson of today, we hope you enjoyed it! See you in the next one!