Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Multiplying and Dividing Monomials
Welcome to our lesson on multiplying and dividing monomials! This fundamental algebra skill is crucial for your mathematical journey. Let's start with the introduction video, which will give you a clear visual understanding of these operations. Monomials are expressions with a single term, like 5x² or -3y. When multiplying monomials, we combine like terms and add exponents. For division, we subtract exponents instead. These operations follow specific rules that, once mastered, will make solving complex algebraic problems much easier. Remember, practice is key to becoming proficient in handling monomials. As we progress, you'll see how these skills apply to more advanced topics in algebra. Don't worry if it seems challenging at first with patience and persistence, you'll soon be multiplying and dividing monomials with confidence. Let's dive in and explore these exciting concepts together!
When you combine like terms, it simplifies the expression and makes it easier to work with. This is especially useful when dealing with polynomials. Additionally, mastering these skills will aid in solving algebraic problems that involve more than one variable. Keep practicing, and you'll find that these techniques become second nature.
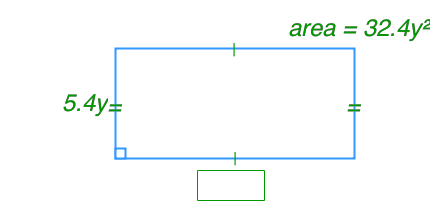
Model and calculate each multiplication. (6x)(2x)
Step 1: Introduction to Multiplying Monomials
Hi, welcome to this question right here. In this section, we are going to model and calculate the multiplication of two monomials. The given problem is (6x)(2x). To solve this, we will first perform the multiplication and then create a model to represent it.
Step 2: Perform the Multiplication
Let's start by performing the multiplication. We have 6x multiplied by 2x. When multiplying monomials, we multiply the coefficients (numbers) together and then multiply the variables together. So, we take the number 6 and multiply it by 2, which gives us 12. Next, we multiply the variables x and x. Since they have the same base, we add their exponents. Each x has an exponent of 1, so 1+1=2. Therefore, x⋅x=x2. Combining these results, we get 12x2.
Step 3: Understanding the Exponents
It's important to understand why we add the exponents when multiplying variables with the same base. In our example, x has an implicit exponent of 1. When we multiply x by x, we are essentially adding the exponents: x1⋅x1=x1+1=x2. This rule applies to any variables with the same base.
Step 4: Creating a Model
To create a model that represents this multiplication, we can use visual aids. Imagine we have two sets of rectangles. The first set represents 2x, and the second set represents 6x. We can use different colors to distinguish between them. For instance, we can use green to represent the positive values.
Step 5: Visual Representation
Let's draw the model. We start by drawing two rectangles to represent 2x. Next, we draw six rectangles to represent 6x. When we multiply these sets together, we get a grid of rectangles. Each intersection of the 2x and 6x rectangles represents x2. Since we have 2 rows and 6 columns, we end up with 12 rectangles, each representing x2. Therefore, the model visually confirms our calculation of 12x2.
Step 6: Final Thoughts
By following these steps, we have successfully multiplied the monomials 6x and 2x to get 12x2. We also created a visual model to represent this multiplication. Remember, the key steps are to multiply the coefficients and add the exponents of the variables. This method can be applied to any similar problems involving the multiplication of monomials.
Q1: What is a monomial?
A monomial is an algebraic expression that consists of a single term. It can be a number, a variable, or a product of a number and one or more variables with non-negative integer exponents. Examples include 5, 3x, -2y³, and 4xy.
Q2: How do you multiply monomials?
To multiply monomials, follow these steps: 1) Multiply the coefficients, 2) Keep all variables, and 3) Add the exponents of like variables. For example, (3x²) * (2x³) = 6x, because 3 * 2 = 6, and the exponents of x are added: 2 + 3 = 5.
Q3: What's the rule for dividing monomials?
When dividing monomials, follow these steps: 1) Divide the coefficients, 2) Keep all variables, and 3) Subtract the exponents of like variables. For instance, (12x) ÷ (3x²) = 4x², because 12 ÷ 3 = 4, and the exponents of x are subtracted: 4 - 2 = 2.
Q4: How do you handle negative exponents when simplifying monomials?
When you encounter negative exponents while simplifying monomials, move the term with the negative exponent to the opposite side of the fraction bar and make the exponent positive. For example, x² can be written as 1/x².
Q5: What are some common mistakes to avoid when working with monomials?
Common mistakes include: forgetting to multiply or divide coefficients, adding exponents when multiplying instead of adding them, subtracting exponents when dividing instead of subtracting them, mishandling negative signs, and forgetting that any non-zero number raised to the power of 0 equals 1. Always double-check your work and practice regularly to avoid these errors.
Understanding the fundamentals of algebra is crucial when tackling more advanced concepts like multiplying and dividing monomials. To excel in this area, it's essential to have a solid grasp of several prerequisite topics that form the foundation of algebraic operations.
One of the most fundamental skills is dividing integers. This basic arithmetic operation is the stepping stone to working with more complex algebraic expressions. Similarly, the application of integer operations provides a practical context for understanding how these concepts apply in real-world scenarios.
As you progress, adding and subtracting polynomials becomes a crucial skill. This topic introduces the concept of like terms and lays the groundwork for more complex polynomial operations. Understanding common factors of polynomials is also vital, as it helps in simplifying expressions and identifying patterns in algebraic structures.
The negative exponent rule is another key concept that plays a significant role in manipulating monomials. This rule is essential when dealing with division operations involving monomials with negative exponents. Additionally, knowing how to multiply a monomial by a binomial serves as a precursor to more complex multiplication of algebraic expressions.
For those looking to advance further, simplifying rational expressions and understanding restrictions is crucial. This topic builds upon the skills of multiplying and dividing monomials and extends to more complex rational expressions. Similarly, adding and subtracting rational expressions requires a solid understanding of monomial operations as a foundation.
While it may seem unrelated at first, knowledge of distance and time related questions in linear equations can provide practical applications for monomial operations, helping to contextualize these abstract concepts in real-world problems.
Lastly, although more advanced, familiarity with the fundamental theorem of algebra offers a broader perspective on algebraic principles, including the behavior of polynomials and their factors, which can deepen your understanding of monomial operations.
By mastering these prerequisite topics, students will find themselves well-equipped to tackle the challenges of multiplying and dividing monomials with confidence and precision. Each concept builds upon the last, creating a strong foundation for advanced algebraic thinking and problem-solving skills.