Sign In
Sign Up
flag-au

Mastering Arcs of a Circle: From Basic Concepts to Advanced Applications
Dive into the world of circular arcs! Learn to calculate arc lengths, understand different types, and explore real-world applications. Boost your geometry skills with our comprehensive guide.

  1. Intros0/2 watched
  2. Examples0/8 watched
  1. 0/2
  2. 0/8
Now Playing:Arcs of a circle – Example 0a
Intros
0/2 watched
  1. Terms related to circles
    • Radius
    • Diameter
    • Circumference
    • Central angle
      • minor arc
      • major arc
    • Inscribed angle
    • Chord
      • perpendicular bisector
    • Tangent
      • point of tangency
  2. How to find the length of an arc?
    • by Central angle
    • by Proportion
    • by Using formula a = Θr

Examples
0/8 watched
  1. Find the length of the arc in red.

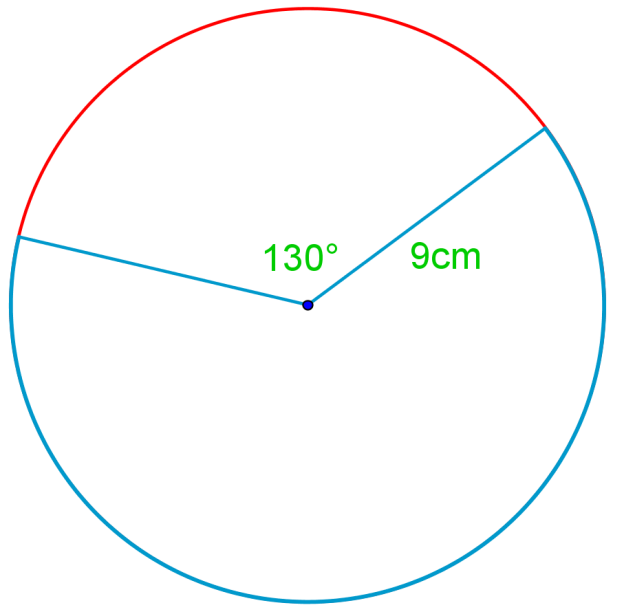
    1. Finding arcs of a circle given radius and angle


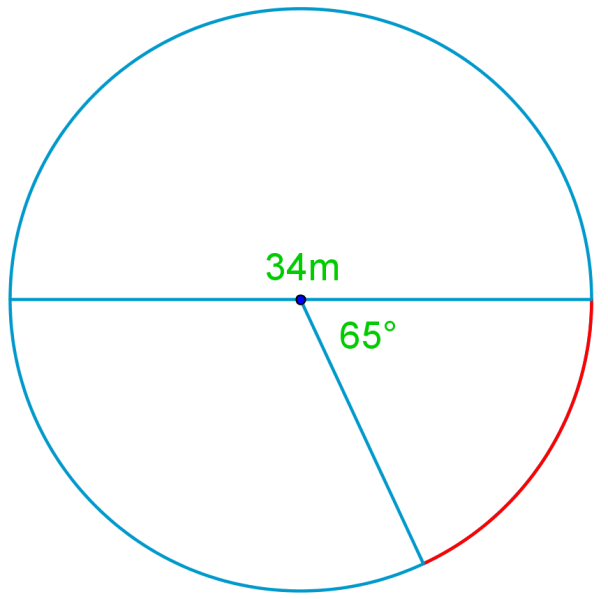
    2. Calculate the arc length using the given angle and diameter


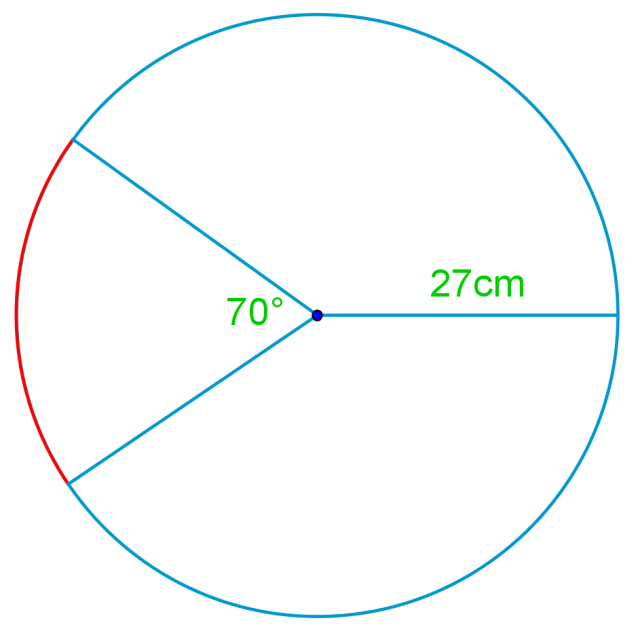
    3. Relationship among arcs of a circle, angle, and radius

Circle and circumference
Jump to:NotesConceptFAQsPrerequisites
Notes
Concept

Introduction to Arcs of a Circle

Welcome to our exploration of arcs of a circle! This fundamental concept in circle terminology is crucial for understanding more advanced geometric principles. An arc is simply a portion of the circumference of a circle, and it's a key element in many mathematical calculations. In our introduction video, we'll dive deep into what arcs are, how they're measured, and their relationship to other parts of a circle. This video is an essential starting point for grasping the concept fully. As we progress, you'll see how arcs play a vital role in various real-world applications, from architecture to engineering. Remember, mastering arcs is like unlocking a new level in your geometry skills! Don't worry if it seems challenging at first with practice and patience, you'll soon become comfortable working with arcs. So, let's get started on this exciting journey through circle terminology, beginning with these fascinating curved segments!

FAQs

Here are some frequently asked questions about arcs of a circle:

1. What is the formula for the arc length of a circle?

The formula for arc length is L = (θ / 360°) × 2πr, where L is the arc length, θ is the central angle in degrees, and r is the radius of the circle. For angles in radians, the formula simplifies to L = θr.

2. How do you find the length of the arc of a circle?

To find the length of an arc, you need to know the radius of the circle and the central angle that subtends the arc. Use the formula L = (θ / 360°) × 2πr, where θ is the central angle in degrees. If you have the angle in radians, use L = θr.

3. What is the formula for the area of an arc?

The area of a sector (region bounded by an arc and two radii) is given by A = (θ / 360°) × πr², where θ is the central angle in degrees and r is the radius. This isn't the area of the arc itself, but the area of the sector it defines.

4. What are the three types of arcs?

The three main types of arcs are: 1) Minor arc: less than half the circumference, 2) Major arc: more than half the circumference, and 3) Semicircle: exactly half the circumference. Each type is defined by the central angle it subtends.

5. How many arcs are there in a circle?

There are infinitely many arcs in a circle. Any two points on a circle's circumference define two arcs - a minor arc and a major arc. As you can choose any two points on the circumference, there are infinitely many possible arcs.

Prerequisites

Understanding the arcs of a circle is a crucial concept in geometry, but to fully grasp this topic, it's essential to have a solid foundation in several prerequisite areas. These fundamental concepts not only provide the necessary background knowledge but also help in developing a deeper understanding of circular arcs and their properties.

One of the most important prerequisites is circles and circumference. Knowing how to calculate the circumference of a circle is vital because arcs are portions of the circle's circumference. This knowledge allows students to relate the length of an arc to the overall circumference, providing a crucial context for understanding arc measurements.

Another key concept to master is central and inscribed angles in circles. The central angle of a circle directly corresponds to the arc it subtends, making this relationship fundamental to working with arcs. Understanding how central angles relate to arc measures is essential for solving problems involving circular arcs.

Chord properties are also closely related to arcs. Chords are line segments that connect two points on a circle's circumference, and their properties often intersect with arc-related concepts. For instance, the perpendicular bisector of a chord always passes through the center of the circle and bisects the arc subtended by the chord.

Similarly, tangent properties play a role in understanding arcs. Tangents are lines that touch the circle at exactly one point, and their properties can be useful in solving problems that involve both tangents and arcs, especially in more advanced geometric constructions.

For those delving deeper into calculus applications, knowledge of the arc length of polar curves becomes relevant. While this may seem advanced, understanding the arc length formula in simpler contexts can provide valuable insights into how arcs behave and are measured in more complex scenarios.

Lastly, proficiency in converting between degrees and radians is crucial when working with arcs. Arcs can be measured in both degrees and radians, and the ability to convert between these units is essential for solving a wide range of problems involving circular arcs.

By mastering these prerequisite topics, students will find themselves well-equipped to tackle the complexities of arcs in circles. Each of these concepts contributes to a comprehensive understanding of circular geometry, allowing for a smoother transition into more advanced topics and applications involving arcs. Remember, a strong foundation in these areas will not only make learning about arcs easier but will also enhance overall problem-solving skills in geometry and related fields.