Sign In
Sign Up
flag-au

Cylindrical Coordinates: Revolutionize Your 3D Math Understanding
Unlock the power of cylindrical coordinates! Master conversion techniques, explore real-world applications, and enhance your spatial reasoning skills. Perfect for physics, engineering, and advanced mathematics.

  1. Intros0/3 watched
  2. Examples0/7 watched
  1. 0/3
  2. 0/7
Now Playing:Cylindrical coordinates – Example 0a
Intros
0/3 watched
  1. Cylindrical Coordinates Overview:
  2. Cylindrical Coordinates Overview:
    What are Cylindrical Coordinates?
    • Instead of (x,y,z{x}, {y}, {z}), we have (r,θ,z{r},\theta, {z})
    • Graph of the coordinates in 3D
  3. Cylindrical Coordinates Overview:
    Equations to Convert from Cartesian to Cylindrical
    • Finding the Equations
    • Ignoring z{z}
    • Trig Ratios, Angles, and Pythagoras Theorem
Examples
0/7 watched
  1. Convert the following Cartesian point into Cylindrical Coordinates:

    (1,3,5)(1,3,5)
    3-D coordinate system
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    Notes:

    Instead of Cartesian coordinates, we use cylindrical coordinates for situations you will see in future sections.
    For now, we will just learn how to convert from 3D Cartesians coordinates to 3D cylindrical coordinates, and vice versa. In other words,

    (x,y,z)→(r,θ,z) (x,y,z) \to (r, \theta, z )

    Suppose we have the following graph:
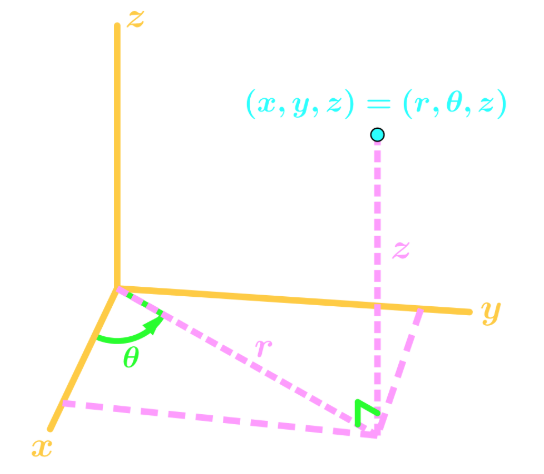
    graph example 3D
    Since the z coordinate doesn't change from converting, we will just focus on the x and y. Thus, we make it into 2D graph:
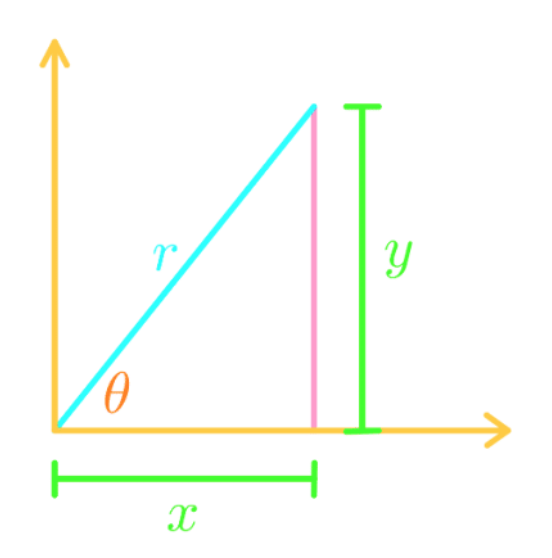
    graph example 2D
    From this graph, we can get the following equations:

    x=rcos⁡θx = r\cos\theta
    y=rsin⁡θy = r\sin\theta
    x2+y2=r2x^2 + y^2 = r^2
    tan⁡−1(yx)=θ\tan^{-1} (\frac{y}{x}) = \theta

    These equations will be useful when converting 3D coordinates.
    Concept

    Introduction to Cylindrical Coordinates

    Cylindrical coordinates offer an alternative way to describe points in 3D space, complementing the familiar Cartesian coordinate system. The introduction video provides a clear and concise explanation of this concept, making it accessible to learners. Unlike Cartesian coordinates (x, y, z), cylindrical coordinates use (r, θ, z), where r represents the distance from the z-axis, θ is the angle in the xy-plane, and z remains the vertical distance. This system is particularly useful for describing objects with circular symmetry or rotational properties. Understanding different coordinate systems is crucial in 3D space, as it allows for more efficient problem-solving in various fields such as physics, engineering, and computer graphics. Cylindrical coordinates often simplify calculations and representations of certain shapes and phenomena, providing a valuable tool alongside Cartesian coordinates. Mastering these systems enhances spatial reasoning and opens up new perspectives in analyzing and describing three-dimensional objects and scenarios.

    FAQs

    Here are some frequently asked questions about cylindrical coordinates:

    1. What are the main advantages of using cylindrical coordinates?

      Cylindrical coordinates offer several advantages, especially when dealing with objects or systems with circular symmetry. They simplify calculations for cylindrical shapes, make it easier to describe rotational motion, and can simplify certain types of integrals in calculus. For example, finding the volume of a cylinder or analyzing the electric field around a wire is often more straightforward in cylindrical coordinates.

    2. How do you convert from Cartesian to cylindrical coordinates?

      To convert from Cartesian (x, y, z) to cylindrical (r, θ, z) coordinates:
      r = (x² + y²)
      θ = tan¹(y/x)
      z remains the same Remember to consider the appropriate quadrant when calculating θ.

    3. In which fields are cylindrical coordinates commonly used?

      Cylindrical coordinates are widely used in physics (e.g., electromagnetic theory, fluid dynamics), engineering (e.g., designing cylindrical structures, analyzing stress in pipes), and mathematics (e.g., solving certain types of integrals). They're particularly useful in any situation involving circular symmetry or rotational motion.

    4. What's the difference between cylindrical and spherical coordinates?

      While both are alternatives to Cartesian coordinates, cylindrical coordinates use (r, θ, z), where r is the distance from the z-axis, θ is the angle in the xy-plane, and z is the height. Spherical coordinates use (ρ, θ, φ), where ρ is the distance from the origin, θ is the azimuthal angle in the xy-plane, and φ is the polar angle from the z-axis. Cylindrical coordinates are best for cylinder-like objects, while spherical coordinates are ideal for sphere-like objects.

    5. How can I visualize points in cylindrical coordinates?

      To visualize a point in cylindrical coordinates (r, θ, z), imagine standing on a circular disk. The r-coordinate is how far you walk from the center, θ is how far you've rotated around the center (counterclockwise from the x-axis), and z is how high you are above or below the disk. This mental image can help in understanding and working with cylindrical coordinates.

    Prerequisites

    Understanding cylindrical coordinates is crucial in various fields of mathematics and physics. However, to fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. These fundamental areas of study provide the necessary tools and insights to comprehend and apply cylindrical coordinates effectively.

    One of the key prerequisites is the knowledge of trigonometric functions. These functions play a vital role in describing the angular component of cylindrical coordinates. Familiarity with trigonometric relationships allows students to navigate the circular nature of this coordinate system with ease.

    The Pythagorean theorem is another cornerstone in understanding cylindrical coordinates. This fundamental principle helps in relating the radial distance to the Cartesian coordinates, forming a bridge between different coordinate systems. Its applications are particularly useful when converting between cylindrical and rectangular coordinates.

    Speaking of coordinate systems, proficiency in converting between coordinate systems is indispensable. While this skill is often associated with unit conversions, the principles apply directly to transforming points between cylindrical, spherical, and Cartesian coordinates. This ability allows for a more versatile approach to problem-solving in three-dimensional space.

    An understanding of circular motion analysis provides valuable insights into the behavior of objects described in cylindrical coordinates. This knowledge helps in visualizing and interpreting the radial and angular components of motion, which are fundamental aspects of the cylindrical coordinate system.

    Lastly, familiarity with rotational symmetry enhances the appreciation of cylindrical coordinates' elegance in describing rotationally symmetric objects and phenomena. This concept aids in recognizing patterns and simplifying problems that exhibit symmetry around an axis.

    By mastering these prerequisite topics, students build a robust foundation for exploring cylindrical coordinates. This background knowledge not only facilitates a smoother learning experience but also enables a deeper understanding of the subject's applications in fields such as engineering, physics, and advanced mathematics. The interconnectedness of these topics highlights the importance of a comprehensive approach to mathematical education, where each concept serves as a stepping stone to more advanced ideas.

    In conclusion, the journey to mastering cylindrical coordinates is paved with these essential prerequisite topics. Each one contributes uniquely to the overall understanding, providing the necessary tools and perspectives to tackle complex problems in three-dimensional space. As students progress in their studies, they'll find that this solid foundation in prerequisite topics not only aids in grasping cylindrical coordinates but also opens doors to further advanced mathematical concepts and their real-world applications.