Bernoulli Equations
In the past sections we have worked through techniques which solve first order linear differential equations but now the time has come for us to take a look at methodology on how to solve equations that are not linear since realistically speaking, we will not always encounter the same type of equations in our path.
Let us first remind ourselves about the difference between a linear and a non-linear differential equation. In basic algebra a linear equation is the one in which its independent variable's order is one, in other words, the variable appears, either by itself or accompanied by a constant coefficient where the exponent of the variable is one. And so, a non-linear equation would be the one where the variable has exponents different than one. For the case of linear differential equations the function can appear by itself, accompanied by coefficients or you can have the derivatives of the function. The equation will be linear as long as the variable and its derivatives have exponents equal to one, if that is not the case, then the equation is non-linear.
Example:
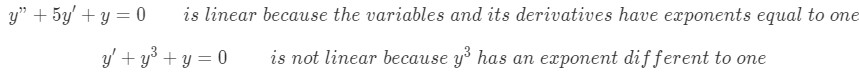
We may be inclined to rapidly conclude that non-linear differential equations are much more complicated to solve than linear equations but, do not resent them yet. Although this statement is true for most cases, efficient and intuitive enough mathematical techniques have been developed to resolve certain non-linear differential equations in a clear and relatively straightforward manner. Thus, you will be pleasantly surprised by the realization that you should already know most of the material that will be covered on this lesson, and that the first technique we would like to study uses a simplification approach, this method makes use of something called Bernoulli equations to transform the original non-linear equations in a problem into something we can solve right away, and for this reason, the Bernoulli equation method includes just a few more steps than the techniques we have been looking so far to solve linear differential equations.
You will see throughout this article that we will extensively review topics we have seen in past sections since the method to solve a differential equation through the Bernoulli equation is just a mathematical trick to simplify a somewhat unconventional equation into a simpler case we already know how to solve. For that reason, we recommend that if you have not studied the integrating factor method to solve first order exact differential equations yet, you take a look into both sections before you continue with this lesson.
By now, it is also important for you to have mastered skills such as the separable equations technique. If you think you need a quick review on it, do not hesitate to go back and check examples on it.
What is the Bernoulli equation?
A Bernoulli differential equation is a non-linear first order differential equation which can be reduced to a linear first order differential expression. The special case for these equations is that they have known exact solutions, and after you have done the transformation into the linear expression you can solve the equation by the integrating factor method with exact equations. The general form of a Bernoulli equation looks as follows:
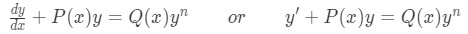
Where n cannot be equal to 0 or 1, since any of these two exponents would result in a linear differential equation expression, and therefore, the Bernoulli equation method would not be needed.
How to solve Bernoulli equations
In order for us to list step by step instructions on how to solve Bernoulli differential equations we will start by using the general form of the equations to give a rough idea of the process, then we will go through a full example that you can also find on the videos for this section.
-
Starting with equation 2, which is a nonlinear differential expression, we select the highest order term and divide the whole expression by it:
Notice that to obtain the equation above.
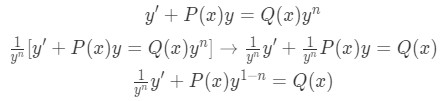
Equation 3: Solving Bernoulli equations part 1 -
We use a substitution to transform the non-linear equation into a linear one:
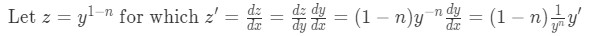
Equation 4: Substitutions to transform from nonlinear to linear -
Plugging this into the nonlinear equation will result in a linear differential expression! You can see the development of this substitution below, and notice how the expression has been rearranged to its simplest form for practical purposes:
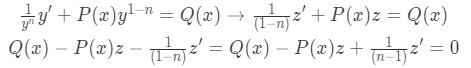
Equation 5: Solving Bernoulli equations part 2 - transformation to a linear differential equation -
And we are left with a linear equation of the form
Which can be easily solved using an integrating factor!
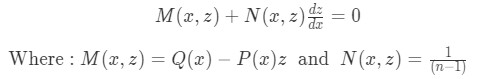
Equation 6: Identifying M and N terms of the differential equation
So as you can see the Bernoulli equation method is just a way to transform the non-linear expression into a linear one, afterwards, we continue to solve the linear differential equation with methodology we have already learned in past sections. There are a few details that need to be taken into account and followed closely while we work through these kind of problems, and therefore, for the purpose of observing the whole process in action, let us work through our first Bernoulli equation example.
Explicitly solve the differential equation:
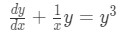
By finding y as a function of x, having the initial condition:
-
Step one:
Start by dividing the whole expression by the highest power of y you can find.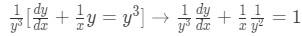
Equation for Example 1(a): Dividing by the highest power -
Step two:
In this case n=3, so we set z and z' and substitute them into the nonlinear equation:
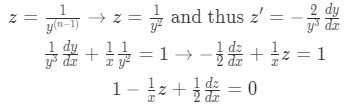
Equation for Example 1(b): Setting z and z' and substituting them into the differential equation Notice this last equation is just the rearranged differential equation after the z substitution. Now you can see that equation for example 1(b) is a linear differential equation of the form: 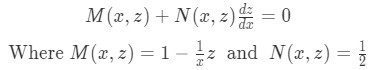
Equation for Example 1(c): identifying M and N in the differential equation -
Step three:
Having a simpler expression, we can now use any of the two methods we have seen in past sections to find the solution for a linear differential equation. So the question is, how do we pick between the method of exact differential equations, and the integrating factor method?
As a general rule, we suggest you try to solve these problems with the method of exact equations first, if it is not possible to find the solution that way, then move onto using an integrating factor.
So we try to solve equation example 1(b) through the exact equations technique. For that, we need to meet the condition that the partial derivative of M with respect to z, is equal to the partial derivative of N with respect to x.
Obtaining the partial derivatives of M and N as follows: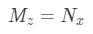
Equation 7. General condition for Exact Differential Equations technique We cannot use the method of exact equations yet, we need to find an integrating factor in order to get an exact equation and continue.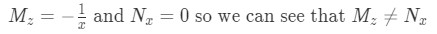
Equation for Example 1(d): Checking to see if the differential equation is exact (is not) -
Step four:
Following the method of integrating factor to find an exact equation to solve for, we multiply equation for example 1(b) for a factor we call "mu of x" (which means this factor denoted by the greek letter "mu" is a function of x).
Notice that since we have simplified the notation of to make the equations look neater.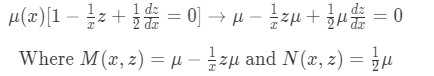
Equation for Example 1(e): Using integrating factor technique to transform the equation into an exact equation Now we check once more for the condition but this time we set it as correct:
We could rapidly (and wrongfully) assume these partial derivatives do not have equal results and so this method would not yield a result. But the thing is that at this point, we do not know what is , and so, what we can conclude here is that in order for our differential equation with an integrating factor to be an exact equation the next condition must be true.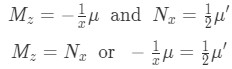
Equation for Example 1(f): Setting the condition to convert the differential equation into an exact equation In order to continue we need to find out what is.
-
Step five:
Solve for using the separable differential equations approach:
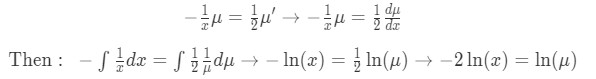
Equation for Example 1(g): Obtaining the value for the integrating factor Applying the exponential to the equation we obtain: -
Step six:
Knowing our integrating factor, we can now multiply it to our equation for example 1(b) and check if we have an exact equation now:
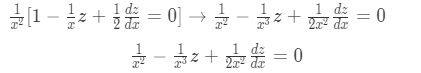
Equation for Example 1(h): Newly found differential equation with integrating factor value Therefore, we now have an exact differential equation and we can use use the method of exact equations to solve the differential equation.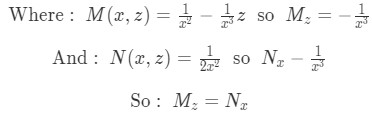
Equation for Example 1(i): Condition met for Exact Equation of the differential equation -
Step seven:
An exact equation is one of the form:
We relate this general form to our equation for example 1(h) where we can see that: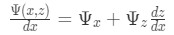
Equation 8: General form of an exact equation And so, we can choose between integrating M or N so we can obtain And so, we can choose between integrating M or N so we can obtain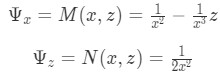
Equation for Example 1(j): Relating our M and N values to the terms found in the general form of an exact equation Now we find f(x) by taking the partial derivative of this equation with respect to x: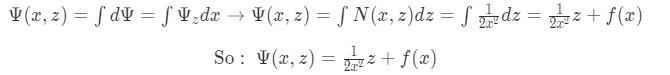
Equation for Example 1(k): Integrating N to find Psi Using the separable equations approach to solve for f(x) so we can find the solution to our equation for example 1(b):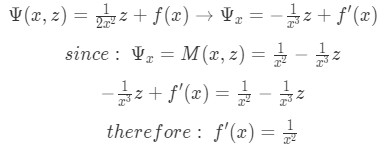
Equation for Example 1(l):Taking the partial derivative of Psi with respect to x to find the unknown function of x 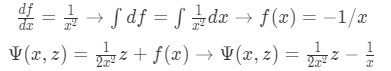
Equation for Example 1(m): Finding f(x) and substituting it into Psi We substitute the expression for z in terms of y:
And we can obtain the final solution to our initial differential equation for example 1:
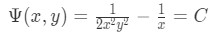
Equation for Example 1(n): Substituting the expression for z to find our final general solution to our initial differential equation -
Step eight:
We input the initial condition to find the explicit solution of equation (a):
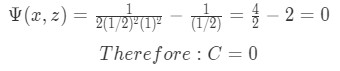
Equation for Example 1(o): Finding the value of C by inputting the initial conditions And so, having solved the original nonlinear differential equation for example 1 with the given conditions we find that:
And we can finally solve for y!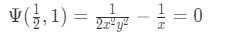
Equation for Example 1(p): Final solution for Psi 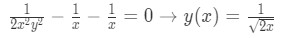
Equation for Example 1(q): Final solution for y If you got to the end, congratulations! Although a little tedious, you probably noticed that except for the first two steps this wasn't new material and hopefully the methodology made sense. We have summarized all of the steps followed in the last pages for the explicit example in the next list, in that way you have a reference to come and check out quickly while you are doing independent study.
Bernoulli Equation Method, Summarized Steps:
1. Divide the expression given by the highest power of y you can find.
2. Identify n, z and z', and substitute z and z' in the original non-linear equation to transform it into a linear expression of the form:
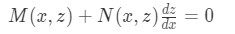
3. Solve the linear differential equation by first checking if is an exact equation. The condition for exact equations says that the partial derivative of M with respect to z, is equal to the partial derivative of N with respect to x. If the condition is met, solve the problem through the exact differential equations method.
4. If the condition is not met, multiply the expression by an integrating factor
- Identify the new M(x,z) and N(x,z) in the expression and obtain their appropriate partial derivatives and set the condition to make the equation "perfect".
5. Solve for using the separable equations method.
6. Multiply our known expression for and check if it meets the condition of an exact equation.
7. If the condition on top is met, solve the equation through the exact equations method.
- Do not forget to substitute the value of z again in the final solution so you end up with a solution in terms of x and y, instead of x and z.
8. If initial conditions are given, use them to find the explicit solution of the equation.
- Do not forget to solve for y at the end.
Solving Bernoulli differential equations
In this section we will be solving examples of Bernoulli differential equations and how we transform them into linear differential equations. Notice that for each case we will only be going through steps 1 and 2 listed above since those are the steps of the transformation from non-linear to linear differential equation. The rest of the steps are mostly a review of exact equations, integrating factor and even separable equations techniques, thus we will keep it simple and only work the steps containing the Bernoulli equation method.
For that same reason, the examples do not contain their explicit solutions.
We recommend you practice how to finish the complete solution for these examples by going through the integrating factor method with exact equations until step seven. You cannot go any further since there will be no conditions given for each of these examples, still, the bulk of the process can be done allowing you to re-study through a few past lessons all at once.
-
Example 2:
Having equation:Divide by the highest power of y: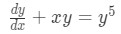
Equation for Example 2: Differential equation to solve Where: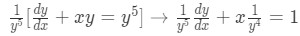
Equation for Example 2(a): Dividing by the highest power of y Substituting and rearranging we obtain the linear equation: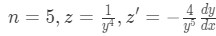
Equation for Example 2(b): Identifying n, z and z' where: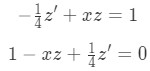
Equation for Example 2(c): Substituting z and z' into the differential equation Solve the now linear differential equation following steps 3 to 8 using techniques such as exact equations, integrating factors and separable equations as needed.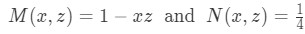
Equation for Example 2(d): Identifying M and N
-
Example 3:
Having equation:Divide by the highest power of y: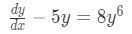
Equation for Example 3: Differential equation to solve Where: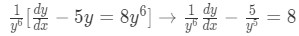
Equation for Example 3(a): Dividing by the highest power of y Substituting and rearranging we obtain the linear equation: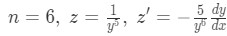
Equation for Example 3(b): Identifying n, z and z' where: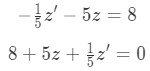
Equation for Example 3(c): Substituting z and z' into the differential equation You have now a linear differential equation to solve looking into steps 3 to 8 and using techniques such as exact equations, integrating factors and separable equations as needed.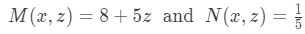
Equation for Example 3(d): Identifying M and N
-
Example 4:
Having equation:Divide by the highest power of y: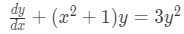
Equation for Example 4: Differential equation to solve Where: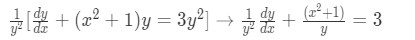
Equation for Example 4(a): Dividing by the highest power of y Substituting and rearranging we obtain the linear equation: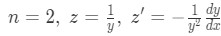
Equation for Example 4(b): Identifying n, z and z' where: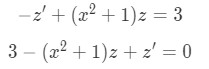
Equation for Example 4(c): Substituting z and z' into the differential equation 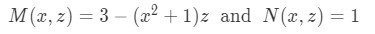
Equation for Example 4(d): Identifying M and N
We finish this article by recommending you to visit the next differential equations notes on the Bernoulli equation, where you can find information and examples (even graphic representations) to complement your understanding for this lesson.
Where both and are both functions of .
To solve this equation first divide the entire equation by
And then we can set
Using implicit differentiation with respect to :
or,
Which we can solve by using our integrating factor technique.






