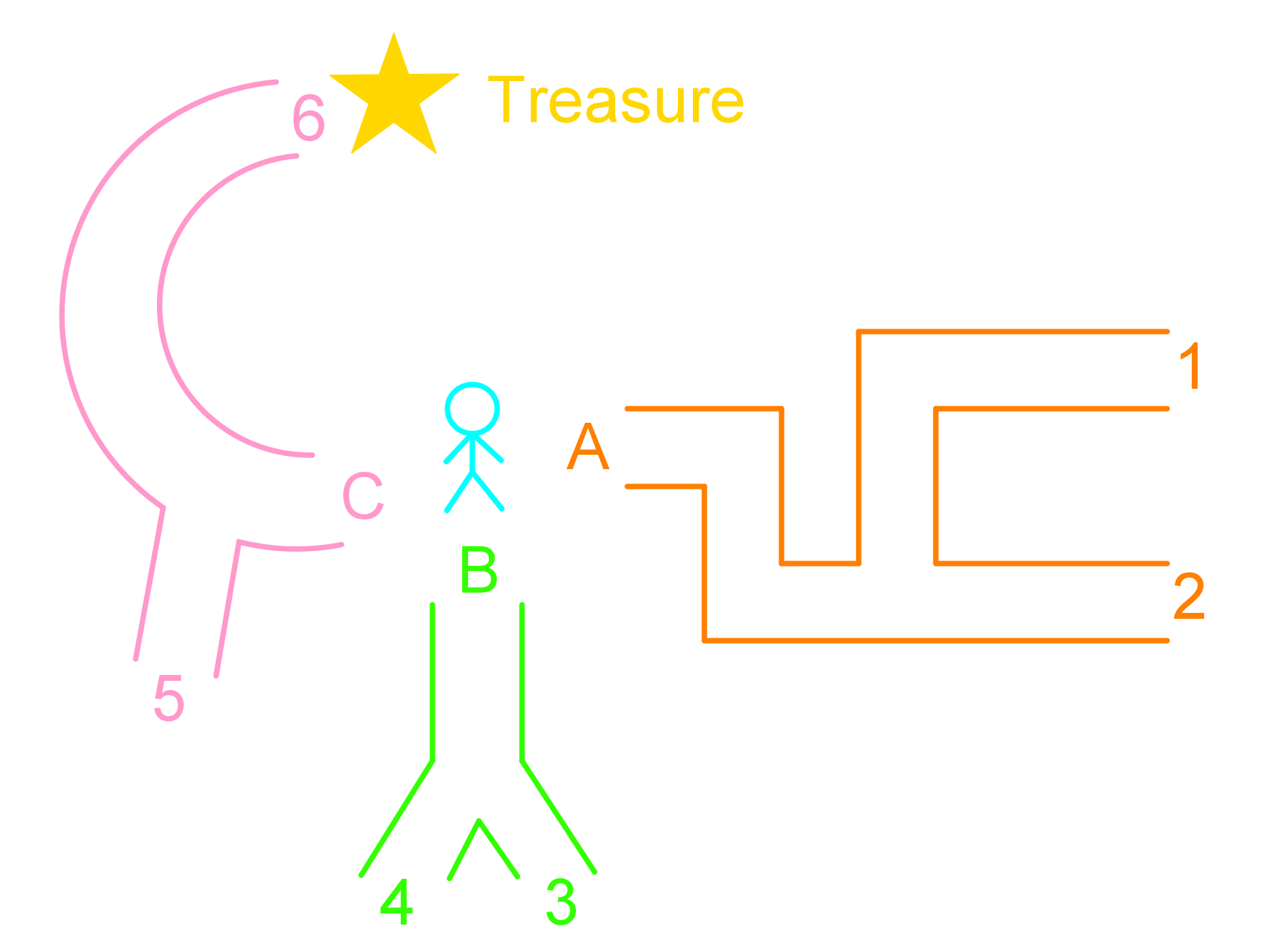
- Sam is hunting a treasure. He is equally likely to travel along any pathway. His trip ends at 1, 2, 3, 4, 5, or 6.
- Claire rolls two 6-sided dice.
- Anna has 18 clothes in her closet. She has 6 shirts, 5 tees, 4 tanks and 3 sweaters. If she is taking 1 top from the closet randomly, what is the probability that:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Probability of Independent Events
Understanding the probability of independent events is a fundamental concept in statistics and probability theory. Our introduction video serves as an excellent starting point for grasping this crucial topic. Independent events are occurrences where the outcome of one event does not affect the probability of another event happening. This concept is essential for accurately calculating probabilities in various real-world scenarios. The video explains how to identify independent events and apply the multiplication rule to determine their combined probability. By mastering this concept, students can tackle more complex probability problems and develop a strong foundation in statistical analysis. The importance of understanding independent events extends beyond academic settings, as it has practical applications in fields such as finance, science, and decision-making. This introduction sets the stage for exploring more advanced probability concepts and their real-world applications.
Sam is hunting a treasure. He is equally likely to travel along any pathway. His trip ends at 1, 2, 3, 4, 5, or 6.

What is the probability that Sam finds the treasure?
Step 1: Understanding the Problem
First, we need to understand the problem. Sam is equally likely to travel along any of the pathways shown in the diagram. His trip can end at one of six possible locations: 1, 2, 3, 4, 5, or 6. We need to determine the probability that Sam finds the treasure, which is located at one of these endpoints.
Step 2: Identifying the Possible Outcomes
Next, we identify all possible outcomes. According to the problem, Sam's trip can end at any of the six locations: 1, 2, 3, 4, 5, or 6. These are our possible outcomes. Since Sam is equally likely to travel along any pathway, each of these outcomes has the same probability of occurring.
Step 3: Determining the Favorable Outcome
We need to determine the favorable outcome, which is the event where Sam finds the treasure. According to the diagram, the treasure is located at endpoint 6. Therefore, the favorable outcome is Sam ending his trip at location 6.
Step 4: Calculating the Probability
To calculate the probability of Sam finding the treasure, we use the formula for theoretical probability. Theoretical probability is calculated as the number of favorable outcomes divided by the total number of possible outcomes. In this case, there is 1 favorable outcome (ending at location 6) and 6 possible outcomes (ending at any of the six locations).
Step 5: Applying the Formula
Using the formula for theoretical probability, we get:
Probability (P) = Number of Favorable Outcomes / Total Number of Possible Outcomes
Substituting the values, we get:
P = 1 / 6
Step 6: Interpreting the Result
The probability that Sam finds the treasure is 1/6. This means that if Sam were to take this trip multiple times, he would find the treasure approximately one out of every six trips. Since the question does not specify that the answer needs to be in a different format, we can leave the probability as a fraction.
-
What are independent events in probability?
Independent events are occurrences where the outcome of one event does not affect the probability of another event happening. For example, flipping a coin and rolling a die are independent events because the result of the coin flip doesn't influence the outcome of the die roll.
-
How do you calculate the probability of two independent events occurring together?
To calculate the probability of two independent events occurring together, you multiply their individual probabilities. This is known as the multiplication rule for independent events. For instance, if the probability of event A is P(A) and the probability of event B is P(B), then the probability of both A and B occurring is P(A) × P(B).
-
What's the difference between independent and dependent events?
Independent events do not affect each other's probabilities, while dependent events do. In independent events, the occurrence of one event doesn't change the probability of the other event. In dependent events, the probability of the second event changes based on the outcome of the first event.
-
Can you give an example of independent events in real life?
A common real-life example of independent events is weather in different cities. The chance of rain in New York doesn't typically affect the chance of rain in Los Angeles on the same day. Another example is drawing cards from a deck with replacement; each draw is independent if you replace the card after each selection.
-
How can tree diagrams help in understanding independent events?
Tree diagrams are visual tools that help represent all possible outcomes of a series of events. For independent events, tree diagrams clearly show how the probability of each branch remains constant, regardless of previous outcomes. They make it easier to visualize and calculate compound probabilities by multiplying probabilities along each path.
When delving into the world of probability, particularly the concept of independent events, it's crucial to have a solid foundation in certain prerequisite topics. These foundational concepts not only enhance your understanding but also provide the necessary tools to tackle more complex probability problems with confidence.
One of the key prerequisites is understanding the exponent product rule. This algebraic concept, which states that (a^x)(a^y) = a^(x+y), might seem unrelated at first glance. However, it plays a vital role in probability calculations, especially when dealing with the multiplication rule for probability. The exponent product rule helps simplify complex probability expressions, making it easier to compute probabilities of multiple independent events occurring together.
Another essential prerequisite is the ability to determine probabilities using tree diagrams and tables. This skill is particularly valuable when working with probability of independent events. Tree diagrams provide a visual representation of different possible outcomes, making it easier to identify and calculate probabilities of specific event combinations. They are especially useful for understanding how probabilities multiply when dealing with independent events.
Mastering these prerequisites will significantly enhance your ability to work with probabilities of independent events. The exponent product rule aids in simplifying calculations, while tree diagrams offer a clear visual method for organizing and computing probabilities. Together, these skills form a strong foundation for tackling more advanced probability concepts.
When studying probability of independent events, you'll find that the multiplication rule for probability is a central concept. This rule states that for independent events A and B, the probability of both occurring is the product of their individual probabilities: P(A and B) = P(A) × P(B). The exponent product rule comes into play here, helping to simplify expressions when dealing with multiple events or repeated trials.
Similarly, tree diagrams for probability become invaluable tools when working with independent events. They allow you to visually map out different scenarios and easily identify the paths that lead to specific outcomes. This visual approach can be particularly helpful in understanding how probabilities combine in more complex situations involving multiple independent events.
By solidifying your understanding of these prerequisite topics, you'll be well-equipped to tackle the intricacies of probability of independent events. You'll find that concepts like the multiplication rule and the use of tree diagrams become more intuitive, allowing you to approach probability problems with greater confidence and accuracy. Remember, a strong foundation in these basics is key to mastering more advanced probability concepts in your future studies.



