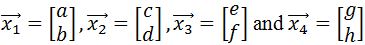 be vertices of a square and be a transformation matrix.
be vertices of a square and be a transformation matrix.Then we can transform the square by combining the vertices into a matrix (denoted by ), and multiply it by the transformation matrix . In other words,
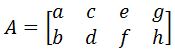
And is the transformed square.
Of course, this idea can also apply to other shapes other than squares.

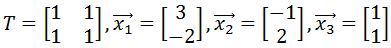
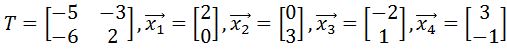
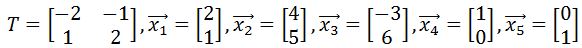
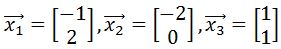 on the graph. Then apply the transformation matrix
on the graph. Then apply the transformation matrix 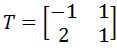 , to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.
, to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.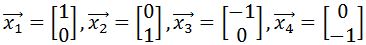 on the graph. Then apply the transformation matrix
on the graph. Then apply the transformation matrix 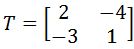 , to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.
, to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.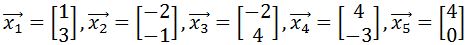 on the graph. Then apply the transformation matrix
on the graph. Then apply the transformation matrix 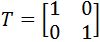 , to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.
, to the vertices to find the transformed polygon, and then plot the transformed polygon on the graph.




