1) The Matrix of Minors
2) The Adjugate
3) Transpose
4) Multiply by
Once we apply these steps, then we will find the inverse.
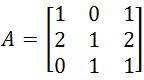 . Find the Matrix of Minors
. Find the Matrix of Minors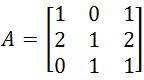 . Find the Adjugate matrix.
. Find the Adjugate matrix. 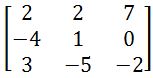 . Transpose this matrix.
. Transpose this matrix.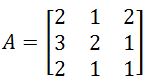 . The transposed adjugate of this matrix is
. The transposed adjugate of this matrix is 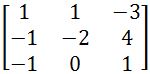 . Find the inverse of A.
. Find the inverse of A.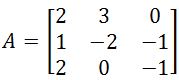 . Find the inverse of this matrix
. Find the inverse of this matrix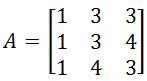 . Find the inverse of this matrix
. Find the inverse of this matrix


Finding the inverse of a 3x3 matrix using determinants and adjugate is a fundamental concept in linear algebra matrix inversion. Our introduction video serves as an essential starting point for understanding this complex topic, providing a clear and concise explanation of the process. This method involves four key steps to find inverse matrix that systematically lead to the inverse matrix. By utilizing determinants, we can determine if the matrix is invertible, while the adjugate matrix plays a crucial role in calculating the inverse. Mastering this technique is vital for solving systems of linear equations, transformations, and various applications in mathematics and engineering. The video breaks down each step, making it easier to grasp the intricacies of matrix inversion. Whether you're a student or professional, understanding how to find the inverse of a 3x3 matrix using determinants and adjugate is an invaluable skill in mathematical problem-solving.
In addition to the theoretical understanding, practical applications of linear algebra matrix inversion are numerous. Engineers and scientists often rely on these methods to solve real-world problems. The four key steps to find inverse matrix include calculating the determinant, finding the matrix of minors, creating the adjugate matrix, and finally, dividing by the determinant. Each of these steps is crucial and must be performed accurately to ensure the correct inverse matrix is obtained. This process is not only important for academic purposes but also for practical applications in various fields. Understanding and mastering these techniques can significantly enhance one's ability to tackle complex mathematical challenges.
Finding the inverse of a 3x3 matrix is crucial in various mathematical and practical applications. It's used in solving systems of linear equations, transformations in computer graphics, and numerous engineering problems. The inverse matrix allows us to "undo" matrix operations, which is essential in many mathematical models and calculations.
No, not all 3x3 matrices can be inverted. A matrix is invertible only if its determinant is non-zero. Matrices with a determinant of zero are called singular matrices and do not have inverses. This is why calculating the determinant is the first step in the inversion process.
The adjugate matrix plays a crucial role in finding the inverse. It's formed by transposing the matrix of cofactors. The adjugate, when multiplied by the reciprocal of the determinant, gives us the inverse matrix. This method is particularly efficient for 3x3 matrices, as it provides a straightforward formula-based approach.
The determinant method (using adjugate) is often more straightforward for 3x3 matrices and provides insight into matrix properties. Row reduction (Gauss-Jordan elimination) is more versatile and efficient for larger matrices. For 3x3 matrices, the choice often depends on personal preference and the specific problem context.
Common mistakes include forgetting to check if the determinant is non-zero, errors in sign changes when calculating cofactors, incorrectly transposing the matrix, and dividing by the determinant instead of multiplying by its reciprocal. Always verify your result by multiplying the original matrix with its calculated inverse to get the identity matrix.
Understanding the inverse of a 3x3 matrix using determinants and adjugates is a complex topic that builds upon several fundamental concepts in linear algebra. To fully grasp this subject, it's crucial to have a solid foundation in prerequisite topics.
One of the most important prerequisites is the determinant of a 2x2 matrix. This concept serves as a stepping stone to understanding determinants of larger matrices, which are essential in calculating matrix inverses. Similarly, familiarity with matrix row operations is vital, as these operations are often used in the process of finding matrix inverses.
A strong grasp of solving systems of linear equations is also crucial. This skill forms the basis for understanding how matrix inverses can be used to solve systems of equations efficiently. Additionally, knowledge of properties of matrix scalar multiplication and properties of matrix addition is essential for manipulating matrices effectively.
The concept of an identity matrix is particularly important when dealing with matrix inverses, as the product of a matrix and its inverse is always the identity matrix. Understanding Cramer's rule can provide valuable insights into the relationship between determinants and matrix inverses.
Moreover, finding the transformation matrix is a related skill that can enhance your understanding of how matrices can represent linear transformations. This concept is closely tied to matrix inverses, as the inverse of a transformation matrix represents the inverse transformation.
Lastly, a solid foundation in linear equation applications can provide real-world context for the importance of matrix inverses and determinants in solving practical problems.
By mastering these prerequisite topics, students will be well-prepared to tackle the complexities of finding the inverse of a 3x3 matrix using determinants and adjugates. Each of these concepts contributes to a comprehensive understanding of matrix operations and their applications, ultimately leading to a deeper appreciation of the power and versatility of linear algebra in solving complex mathematical problems.
