Surface Area and Volume of Prisms: Essential Geometry Concepts

Dive into the world of prisms! Learn to calculate surface area and volume, master key formulas, and apply your skills to real-world problems. Boost your geometry prowess with our comprehensive guide.

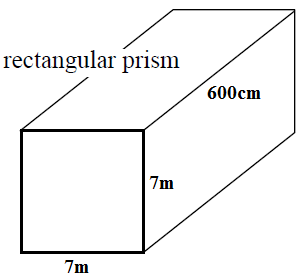
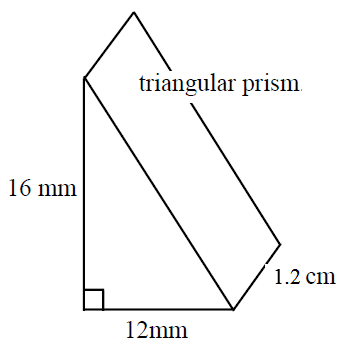
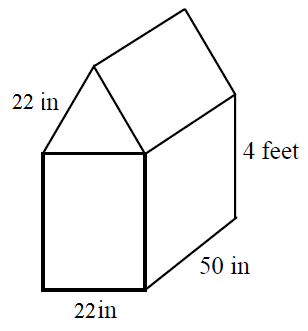
Find the surface area and the volume of the following prisms:

Step 1: Understanding the Shape

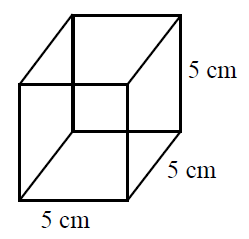
First, identify the shape of the prism. In this case, the prism is a cube. A cube has six identical square faces. This identification is crucial because it simplifies the calculations for both surface area and volume.

Step 2: Finding the Surface Area

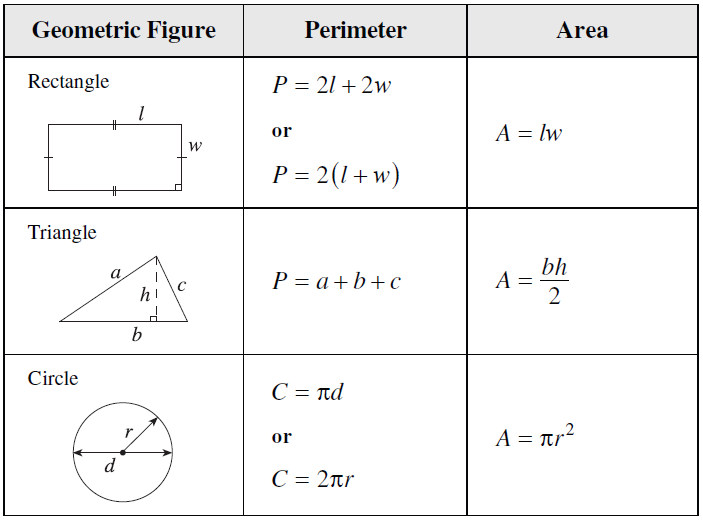
To find the surface area of a cube, you need to calculate the area of one of its square faces and then multiply that by the total number of faces (which is six for a cube).

1. Calculate the area of one face: Since each face is a square, the area of one face is given by the formula side × side (or side²).

2. Multiply by the number of faces: Since a cube has six faces, the total surface area is 6 × (side²).

For example, if the side length of the cube is 5 cm, the area of one face is 5 cm × 5 cm = 25 cm². Therefore, the total surface area is 6 × 25 cm² = 150 cm².

Step 3: Finding the Volume

To find the volume of a cube, you use the formula for the volume of a rectangular prism, which is length × width × height. However, since all sides of a cube are equal, this simplifies to side × side × side (or side³).

1. Calculate the volume: Simply cube the length of one side of the cube.

For example, if the side length of the cube is 5 cm, the volume is 5 cm × 5 cm × 5 cm = 125 cm³.

Step 4: Summary

In summary, to find the surface area and volume of a cube:

• Surface Area: Calculate the area of one face (side²) and multiply by 6.
• Volume: Cube the length of one side (side³).

Using these steps, you can easily determine the surface area and volume of any cube given the length of its sides.

1. What is the difference between surface area and volume of a prism?

   Surface area is the total area of all external faces of a prism, while volume is the amount of space it occupies. For example, in a rectangular prism, surface area includes all six faces, whereas volume is the space inside the prism. Surface area is measured in square units (e.g., cm²), while volume is measured in cubic units (e.g., cm³).

2. How do you calculate the volume of a prism?

   The volume of a prism is calculated using the formula: Volume = Area of Base × Height. This formula works for all types of prisms. For a rectangular prism, it would be length × width × height. For a triangular prism, it would be (1/2 × base × height of triangle) × length of prism.

3. What are some real-world applications of understanding prism surface area and volume?

   Understanding prism surface area and volume is crucial in various fields. In architecture, it helps in designing buildings and calculating material needs. In engineering, it's used for creating efficient packaging solutions. In manufacturing, it aids in determining material requirements and product capacities. Even in everyday life, it's useful for tasks like calculating paint needed for a room or the capacity of storage containers.

4. How does the shape of a prism affect its surface area to volume ratio?

   The shape of a prism significantly affects its surface area to volume ratio. Generally, prisms with more sides (like hexagonal prisms) have a lower surface area to volume ratio compared to prisms with fewer sides (like triangular prisms) of the same volume. This ratio is important in fields like biology, where cell shapes affect nutrient absorption, and in engineering, where it influences heat transfer and material efficiency.

5. Can two prisms have the same volume but different surface areas?

   Yes, two prisms can have the same volume but different surface areas. For instance, a tall, thin rectangular prism and a short, wide rectangular prism might have the same volume, but the taller one will have a larger surface area. This concept is important in design and engineering, where optimizing shape can lead to material savings or improved functionality while maintaining the same volume.

Understanding the surface area and volume of prisms is a crucial concept in geometry that builds upon several fundamental mathematical principles. While there are no specific prerequisite topics provided for this subject, it's important to recognize that a strong foundation in basic geometry and algebra is essential for mastering this topic.

To fully grasp the concepts of surface area and volume of prisms, students should be comfortable with basic geometric shapes, particularly rectangles and triangles. These shapes form the bases and faces of various prisms, and understanding their properties is crucial. Additionally, familiarity with area calculations for 2D shapes is vital, as these skills directly translate to calculating the surface area of prisms.

A solid understanding of basic algebraic concepts is also beneficial when working with surface area and volume formulas. Students should be comfortable manipulating equations and solving for variables, as these skills are often required when applying formulas to real-world problems involving prisms.

Measurement and unit conversion are other important areas that contribute to success in this topic. When calculating surface area and volume, students often need to work with different units of measurement and convert between them accurately.

Spatial reasoning and visualization skills play a significant role in understanding prisms and their properties. The ability to mentally manipulate 3D objects and understand how they relate to 2D representations is crucial for solving problems related to surface area and volume.

While not always explicitly stated as prerequisites, a basic understanding of nets (2D representations of 3D shapes) can greatly enhance a student's ability to conceptualize prisms and calculate their surface areas. Similarly, knowledge of cross-sections can aid in understanding how prisms are formed and how their volumes are calculated.

It's also worth noting that familiarity with different types of prisms, such as rectangular prisms, triangular prisms, and other polygonal prisms, can provide a broader context for applying surface area and volume concepts. This knowledge allows students to recognize and analyze various prism shapes in real-world scenarios.

Lastly, a general understanding of mathematical problem-solving strategies is invaluable when tackling complex surface area and volume problems. This includes skills such as breaking down problems into smaller steps, identifying relevant information, and applying appropriate formulas.

By ensuring a strong foundation in these underlying concepts, students will be better equipped to tackle the challenges presented by surface area and volume of prisms. This topic serves as a stepping stone to more advanced geometric concepts and has practical applications in fields such as architecture, engineering, and design. Therefore, mastering these prerequisites not only aids in understanding prisms but also prepares students for future mathematical endeavors.

• Surface area of prisms
• Volume of prisms

• Word problems relating volume of prisms and cylinders