What is the pythagorean theorem
The pythagorean theorem is a fundamental part of geometry, but what is the pythagorean theorem definition? This theorem—one of many triangle theorems—shows the relationship the three sides of a right triangle has with one another. Labelling the sides touching the right angle as "" and "", and the longer hypotenuse side of the triangle as "", the pythagorean theorem tells us that:
This is the equation that will help you find any side of a right triangle as long as you are given the lengths of the other two sides. It uses the squares of the sides. You're also able to prove that a triangle is a right triangle if you have all the sides and are able to put their lengths nicely into the pythagorean theorem.
What is a hypotenuse
We briefly touched on what the hypotenuse is above, but simply put, the hypotenuse is the longest side of a right triangle. You can find the hypotenuse opposite from the right angle in the triangle itself. It is the only side that is not touching the degrees angle.
How to find the hypotenuse
So you may be wondering: how do I find the hypotenuse? It's simple! You just use the pythagorean theorem above! It is crucial to helping you figure out the hypotenuse in a right angle triangle. You will first need the other two sides before you can figure out the longer hypotenuse side of the triangle, but it's easy once you've got that down!
Example problems
Let's try our hand at using the pythagorean theorem to work out the sides of a triangle with some example problems.
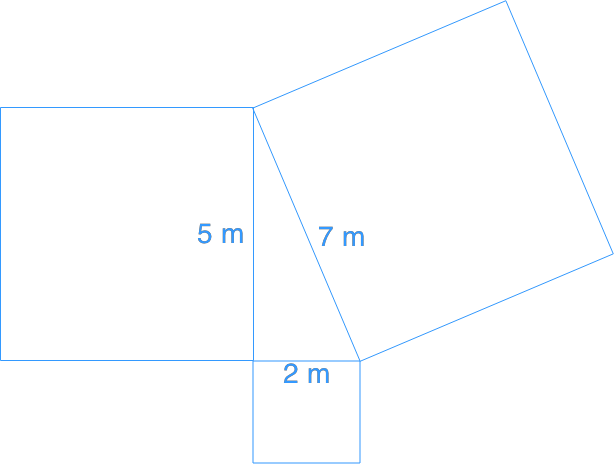
Question 1:
Find the side lengths of the squares.
Solution:
You can see that there is a degree angle in the triangle sandwiched between the three squares. This means we've got a right triangle here, allowing us to use the pythagorean theorem to help us find the answer.
We have two sides given to us, and in order to find the hypotenuse, we can substitute in the numbers into the pythagorean theorem.
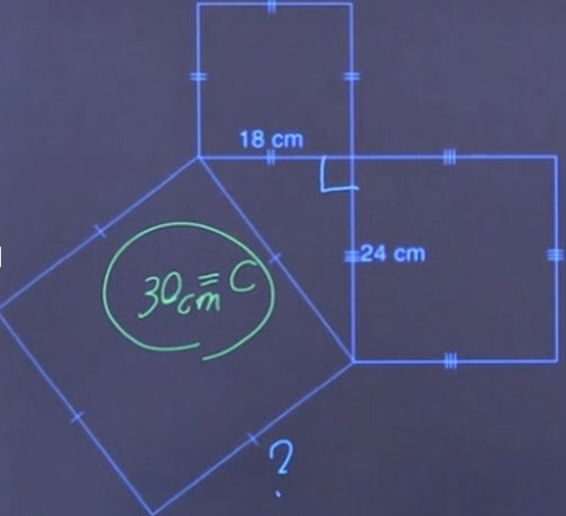
Your final answer is that equals cm.
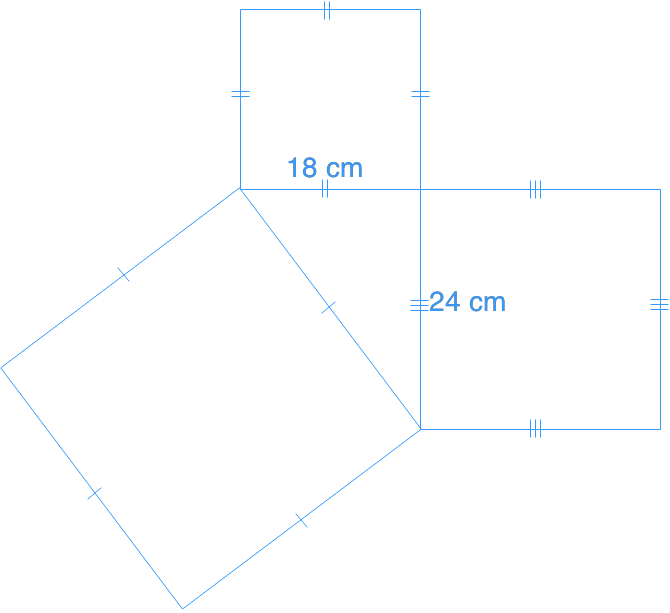
Question 2:
Find .
Solution:
Once again, we've got a right triangle. We're also finding the hypotenuse in this case. Let , which is our hypotenuse.
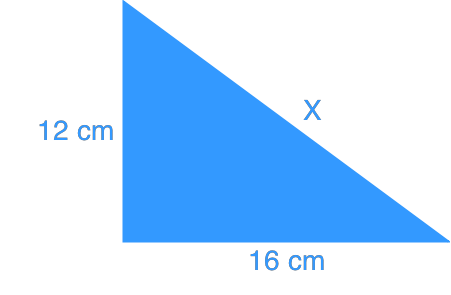
Question 3:
Find x.
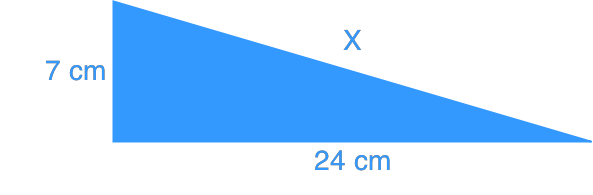
Solution:
You've probably got the hang of the steps by now!
Let
Play around with this online calculator to see how the pythagorean can be used when you scale the sides of a right triangle down or up.
Moving on forward, explore how to use exponents to describe numbers and how you can use the linear function distance formula in math.