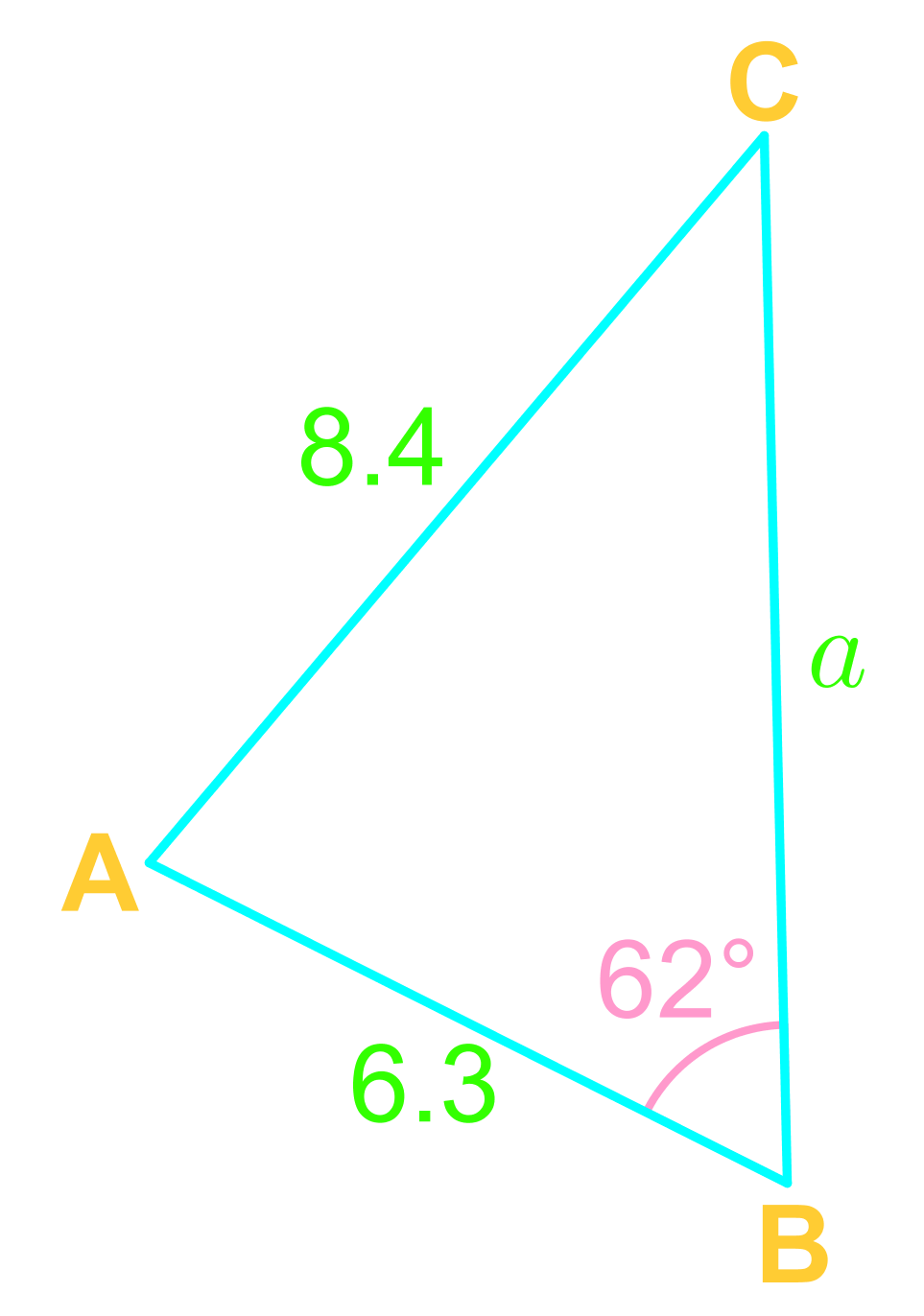
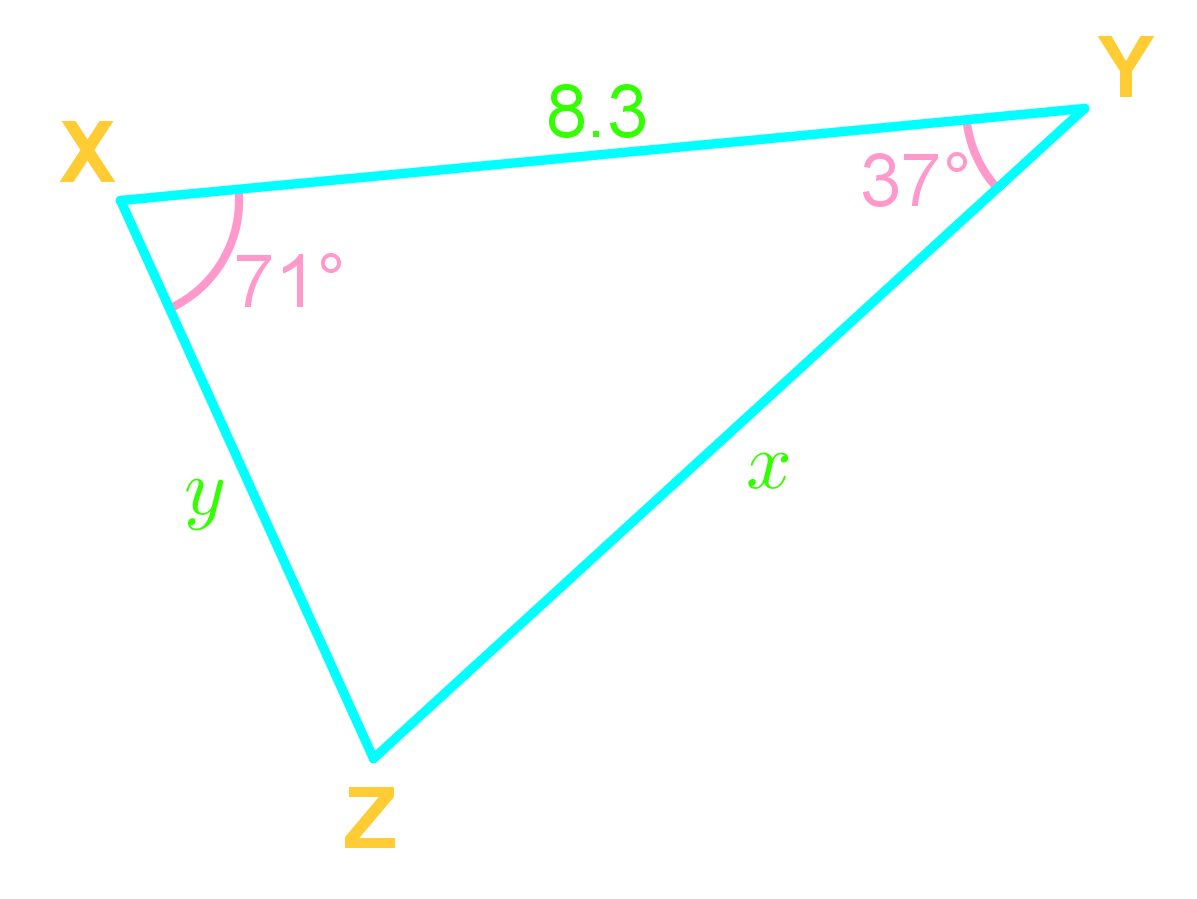
For any ABC,
and,
Use the Law of Sine when given a pair!
Ambiguous case
Ambiguous case of the Law of Sine arises when given SSA (side-side-angle)
Step 1) Use the given angle to find the height of the triangle:
Step 2) Check if,
< , then no triangles
, then 1 triangle
> , then 1 triangle
< < , then 2 triangles
Step 3) Solve the triangle(s)!