Slope Fields consist of a bunch of lines indicating the slope of y with respect to x, or
- Understanding Slope Fields
Find the directional field for the following equations: - Determining the Equation from a Slope Field
Which equation best corresponds to the following slope field?

i. dxdy=y−2
ii. dxdy=xy−2
iii. dxdy=x+1
iv. dxdy=−x+1
- Which equation best corresponds to the following slope field?
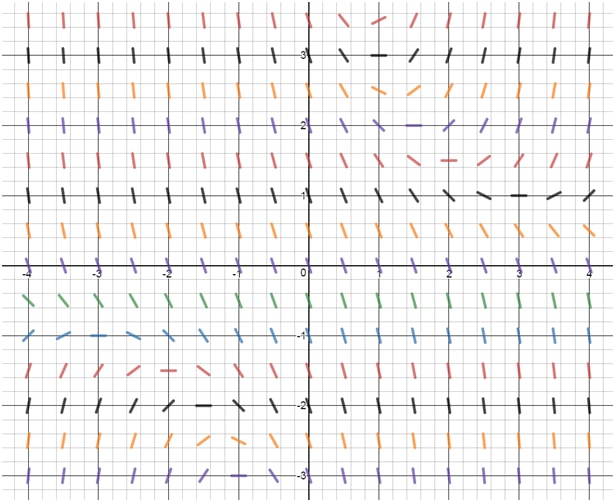
i. dxdy=xy−2
ii. dxdy=−xy
iii. dxdy=2x+y
iv. dxdy=xy−3
- Given the differential equation and its resulting slope field:
dxdy=2y(y−3)

Draw a solution to the following differential equation using the following initial value conditions:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Slope Fields consist of a bunch of lines indicating the slope of y with respect to x, or
Introduction to Slope Fields
Welcome to the fascinating world of slope fields! These powerful tools are essential in solving first-order differential equations, providing a visual representation of solutions without actually solving the equation. Slope fields, also known as direction fields, offer a graphical approach to understanding the behavior of differential equations. By plotting line segments that represent the slope at various points, we can visualize the general shape of solution curves. Our introduction video will guide you through the basics of slope fields, demonstrating how they're constructed and interpreted. This visual aid is crucial for grasping the concept, as it bridges the gap between abstract equations and their real-world applications of differential equations. Whether you're studying physics, engineering, or pure mathematics, mastering slope fields will enhance your problem-solving skills and deepen your understanding of differential equations. So, let's dive in and explore how these remarkable tools can illuminate the path to solving complex mathematical problems!
By plotting line segments accurately, you can better understand the direction and behavior of the solutions. This method is particularly useful in various real-world applications of differential equations, making it a valuable skill for students and professionals alike.
Understanding Slope Fields
Find the directional field for the following equations:
dxdy=xy−x
Step 1: Introduction to Directional Fields
To find the directional field for the given differential equation dxdy=xy−x, we need to understand what a directional field is. A directional field, also known as a slope field, is a graphical representation of the slopes of a differential equation at various points in the plane. It helps visualize the behavior of solutions to the differential equation without solving it explicitly.
Step 2: Setting Up the Equation
The given equation is dxdy=xy−x. To create the directional field, we need to evaluate the slope dxdy at various points (x,y) in the plane. This involves substituting specific values of x and y into the equation to find the corresponding slopes.
Step 3: Evaluating Slopes at Specific Points
Let's start by evaluating the slope at some specific points:
- At (0,0): dxdy=0⋅0−0=0
- At (1,0): dxdy=1⋅0−1=−1
- At (0,1): dxdy=0⋅1−0=0
- At (1,1): dxdy=1⋅1−1=0
- At (−1,1): dxdy=−1⋅1−(−1)=0
Step 4: Analyzing the Slope Patterns
From the points evaluated, we notice that along the y-axis (where x=0), the slope is always 0. This means that the directional field will have horizontal lines along the y-axis. Similarly, along the line y=1, the slope is also 0, indicating horizontal lines along this line as well.
Step 5: Generalizing the Slope Calculation
To generalize the slope calculation, we can consider specific values for x and y and observe the resulting slopes:
- For x=1: dxdy=y−1
- For y=0: dxdy=−x
- For y=2: dxdy=2x−x=x
- For y=−1: dxdy=−x−x=−2x
Step 6: Drawing the Directional Field
Using the slopes calculated in the previous steps, we can now draw the directional field. For each point (x,y), draw a small line segment with the corresponding slope. For example:
- At (1,0), draw a line segment with a slope of -1.
- At (0,1), draw a horizontal line segment (slope 0).
- At (1,1), draw a horizontal line segment (slope 0).
- At (1,2), draw a line segment with a slope of 1.
- At (1,−1), draw a line segment with a slope of -2.
Step 7: Interpreting the Directional Field
The directional field provides a visual representation of the behavior of solutions to the differential equation. By observing the pattern of slopes, we can infer the general shape of the solution curves. For example, horizontal lines along the y-axis and the line y=1 indicate that solutions will have constant slopes in these regions.
Step 8: Conclusion
In conclusion, finding the directional field for the differential equation dxdy=xy−x involves evaluating the slope at various points, generalizing the slope calculation, and drawing the corresponding line segments. This graphical representation helps visualize the behavior of solutions without solving the equation explicitly.
-
What is a slope field?
A slope field, also known as a direction field, is a graphical representation of a first-order differential equation. It consists of short line segments plotted at various points in the xy-plane, indicating the slope of the solution curve at each point. Slope fields provide a visual way to understand the behavior of solutions without explicitly solving the differential equation.
-
How do you create a slope field?
To create a slope field:
- Choose a grid of points in the xy-plane.
- For each point, calculate the slope using the differential equation.
- Draw a short line segment at each point with the calculated slope.
- Repeat for all points in the grid.
The resulting pattern of line segments forms the slope field.
-
What information can be derived from a slope field?
Slope fields provide valuable information about the solutions of differential equations, including:
- The general shape and direction of solution curves
- Locations of equilibrium solutions (where slopes are zero)
- Regions where solutions are increasing or decreasing
- Potential long-term behavior of solutions
- Stability of equilibrium points
-
Can solution curves in a slope field intersect?
No, solution curves in a well-defined slope field cannot intersect. This is because at any given point, there can only be one slope value, which determines the unique direction of the solution curve passing through that point. If two curves were to cross, it would imply two different slopes at the same point, contradicting the definition of a slope field.
-
What are some practical applications of slope fields?
Slope fields have numerous applications across various fields:
- Physics: Modeling motion of objects under forces
- Biology: Analyzing population dynamics and ecological systems
- Economics: Studying market trends and economic growth models
- Engineering: Visualizing behavior of control systems
- Chemistry: Analyzing reaction rates and chemical kinetics
They are particularly useful in situations where qualitative understanding of system behavior is needed without solving complex equations explicitly.
To fully grasp the concept of slope fields, it's crucial to have a solid foundation in several prerequisite topics. Understanding these fundamental concepts will significantly enhance your ability to work with and interpret slope fields effectively.
One of the most important prerequisites is the rate of change. This concept is essential because slope fields visually represent the rate of change of a function at various points in a plane. By mastering rate of change, you'll be better equipped to interpret the direction and steepness of the slopes in a slope field.
Another critical topic to understand is modeling with differential equations. Slope fields are often used to visualize solutions to differential equations, so having a strong grasp of how these equations model real-world phenomena will greatly enhance your understanding of slope fields and their applications.
Equilibrium solutions play a significant role in the analysis of slope fields. These solutions represent steady states in a system and are often visible as horizontal lines in a slope field. Understanding equilibrium solutions will help you identify important features and behaviors within slope fields.
An introduction to nonlinear equations is also valuable when working with slope fields. Many real-world problems involve nonlinear differential equations, and slope fields are an excellent tool for visualizing their solutions. Familiarity with nonlinear equations will help you interpret more complex slope fields accurately.
The concept of continuous growth and decay is particularly relevant to slope fields. Many slope fields represent systems that exhibit growth or decay, such as population models or radioactive decay. Understanding these patterns will allow you to make meaningful connections between the slope field and the underlying phenomena it represents.
Lastly, knowledge of solving differential equations with step functions can be beneficial when working with more advanced slope fields. Step functions can introduce discontinuities in slope fields, and understanding how to handle these situations will broaden your ability to analyze and interpret a wider range of slope fields.
By mastering these prerequisite topics, you'll be well-prepared to tackle slope fields with confidence. Each concept builds upon the others, creating a strong foundation for understanding the behavior of functions and their derivatives in a visual context. As you progress in your study of slope fields, you'll find that your knowledge of these prerequisites will continually reinforce and deepen your understanding of this powerful mathematical tool.



