1. Home
  2. >Algebra
  3. >Matrices
Help

The inverse of 3 x 3 matrix with determinants and adjugate

Everything You Need in One Place

Homework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered.

Learn and Practice With Ease

Our proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals.

Instant and Unlimited Help

Our personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now!

Get the most by viewing this topic in your current grade. Pick your course now.

?
Intros
Lessons
  1. The Inverse of 3 x 3 Matrix Overview:
    a)
    The Matrix of Minors
    b)
    The Adjugate Matrix
    c)
    Transpose
    d)
    Multiply by   1determinant  of  original  matrix\;\frac{1}{determinant\; of\; original\; matrix}
?
Examples
Lessons
  1. Finding the Matrix of Minors
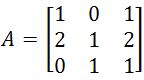    You are given that The inverse of 3 x 3 matrix with determinants and adjugate. Find the Matrix of Minors
    1. Finding the Adjugate Matrix
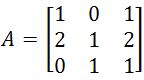      You are given that the matrix of minors is The inverse of 3 x 3 matrix with determinants and adjugate. Find the Adjugate matrix.
      1. Transposing the Adjugate
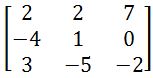        You are given that the Adjugate Matrix is The inverse of 3 x 3 matrix with determinants and adjugate. Transpose this matrix.
        1. Getting the inverse
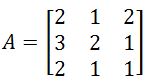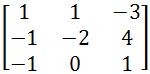          You are given that The inverse of 3 x 3 matrix with determinants and adjugate. The transposed adjugate of this matrix is The inverse of 3 x 3 matrix with determinants and adjugate. Find the inverse of AA.
          1. Applying the 4 steps to get the inverse
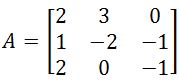            You are given that The inverse of 3 x 3 matrix with determinants and adjugate. Find the inverse of this matrix
            1. Applying the 4 steps to get the inverse
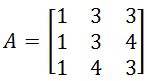              You are given that The inverse of 3 x 3 matrix with determinants and adjugate. Find the inverse of this matrix
              Topic Notes
              ?
              In this lesson, you will learn the long way of computing the inverse of a 3 x 3 matrix. This method requires 4 steps. The first step is the matrix of minor. Each entry in the matrix is a 2 x 2 matrix that is not in that entry's row or column. The second step is the adjugate. This requires you to take your matrix of minors and changing the signs of certain entries depending on the negative signs that appear in the checkerboard. The third step is to transpose. This requires you to switch all the rows and make them into columns. The last step is to multiply your transposed matrix by 1 over the determinant of the original matrix (scalar multiplication). All of these steps should now give you the inverse.
              This method is the long way of computing the inverse of a 3 x 3 matrix. To do this, we need to go through 4 steps:

              1) The Matrix of Minors
              2) The Adjugate
              3) Transpose
              4) Multiply by   1determinant  of  original  matrix\;\frac{1}{determinant\; of\; original\; matrix}

              Once we apply these steps, then we will find the inverse.
              Basic Concepts
              ?
              Related Concepts
              ?