Set notation - Set Theory

Do better in math today
Get Started Now

Set Theory Topics:

Set notation

Lessons

Notes:

In this lesson, we will learn:

  • Drawing Venn Diagrams With Sets
  • Understanding How to Use Set Notation
  • Drawing and Interpreting Venn Diagrams

Notes:

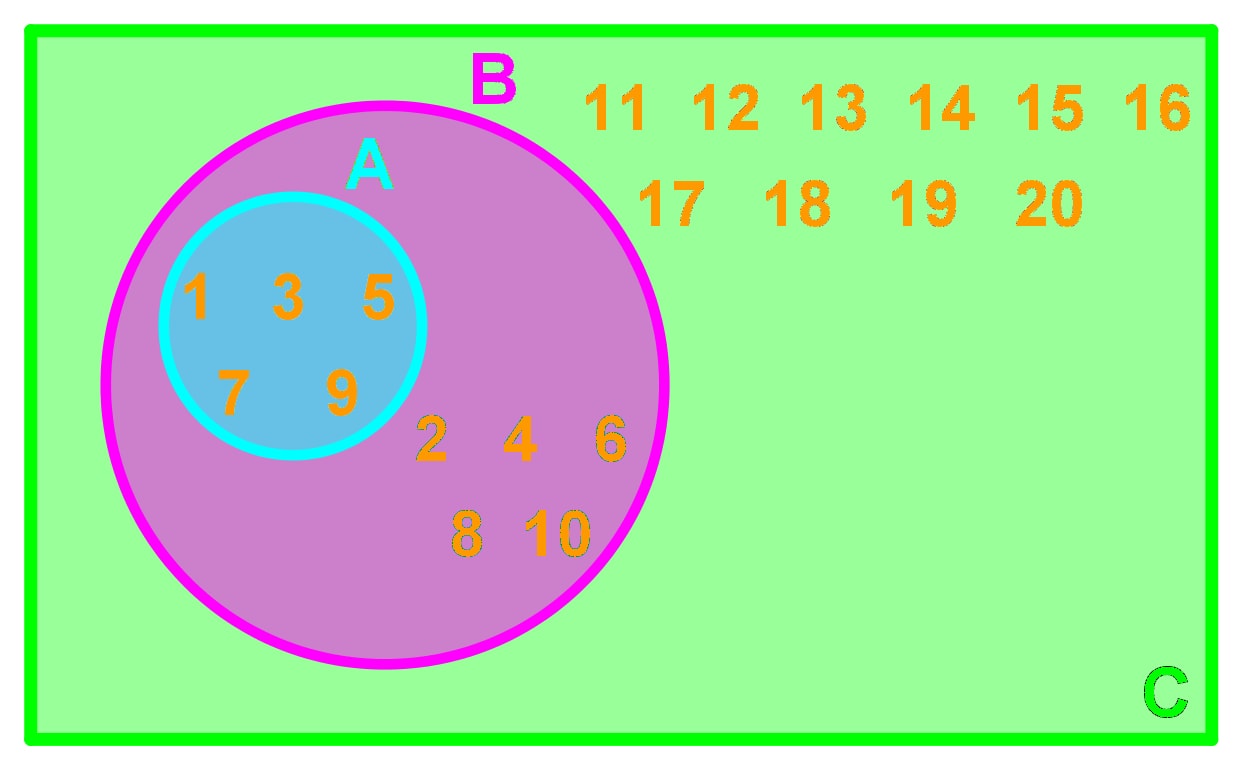
Here are some terms that we need to know for set notations:

Set: A list of objects or numbers.

Element: An object or a number in a set.

n(AA): The number of elements in set AA.

Subset: A set where all its elements belong to another set.

Universal Set: A set of all elements in a particular context.

Empty Set: A set with no elements.

Disjoint: Two or more sets that do not have any elements in common.

Mutually Exclusive: Two or more events that cannot happen simultaneously.

Finite Set: A set with a finite number of elements.

Infinite Set: A set with an infinite number of elements.

Complement: The list of remaining elements in the universal set that is not in the mentioned set. If BB is a set. Then we defined the complement to be B′B' or B‾\overline{B}.

  • 3.
    Drawing and Interpreting Venn Diagrams

    Consider the following information:

    • Universal Set U=U = {−10,−9,−8,−7,−6,−5,−4,−3,−2,−1,0,1,2,3,4,5,6,7,8,9,10}\mathrm\{-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}
    • Set AA = {positive odd number up to 10}
    • Set BB = {positive even number up to 10}
    • Set CC = {0}
Teacher pug

Set notation

Don't just watch, practice makes perfect.

We have over 1850 practice questions in Algebra for you to master.
Get Started Now