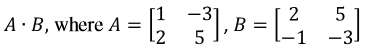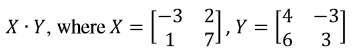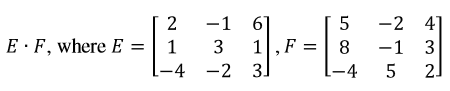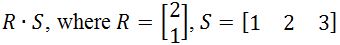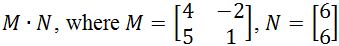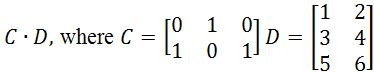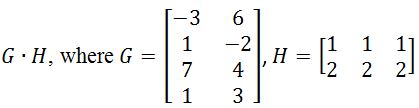Matrix Multiplication
There are exactly two ways of multiplying matrices. The first way is to multiply a matrix with a scalar. This is known as scalar multiplication. The second way is to multiply a matrix with another matrix. That is known as matrix multiplication.
Scalar Multiplication
scalar multiplication is actually a very simple matrix operation. To multiply a scalar with a matrix, we simply take the scalar and multiply it to each entry in the matrix. Let's do an example.
Question 1: Calculate if
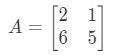
The question is asking us to find out what is. In other words, we are finding
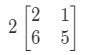
Notice that if we are to multiply 2 to each entry in the matrix, we get that:
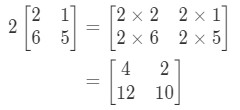
Very simple! Let's do another one.
Question 2: Calculate if
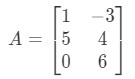
Again, we are trying to find . This means that we will be looking for the answer to
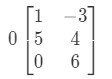
The matrix will be oddly shaped, but the concept remains the same. We will still multiple the scalar 0 to each entry in the matrix. Doing so gives us:
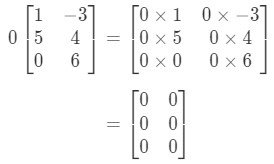
Notice that all the entries in the matrix are 0. This is known as a zero matrix that is 3 x 2.
Now that we are very familiar with scalar multiplication, why don't we move on to matrix multiplication?
How to Multiply Matrices
To multiply a matrix by another matrix, we first need to learn about what dot product is.
What is dot product?
Dot product (also known as vector multiplication) is a way to calculate the product of two vectors. For example, let the two vectors be:
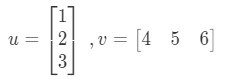
How would I multiply these two vectors? Simply just multiply the corresponding entries, and add the products together. In other words,
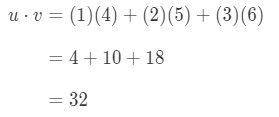
So we get a single value from multiplying vectors. However, notice how that the two vectors have the same number of entries.What if one of the vectors has a different number of entries than the other? For example, let
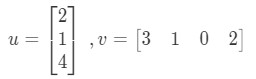
If I were to multiply the corresponding entries and add them up all together, then I get:
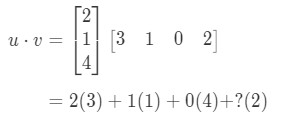
There is a problem here. The first three entries have corresponding entries to multiply with, but the last entry doesn't. So what do we do here? The answer is we cannot do anything here. This just means we cannot calculate the dot product of these two vectors.
So in conclusion, we cannot find the dot product of two vectors that have different numbers of entries. They must have the same number of entries.
2 x 2 Matrix Multiplication
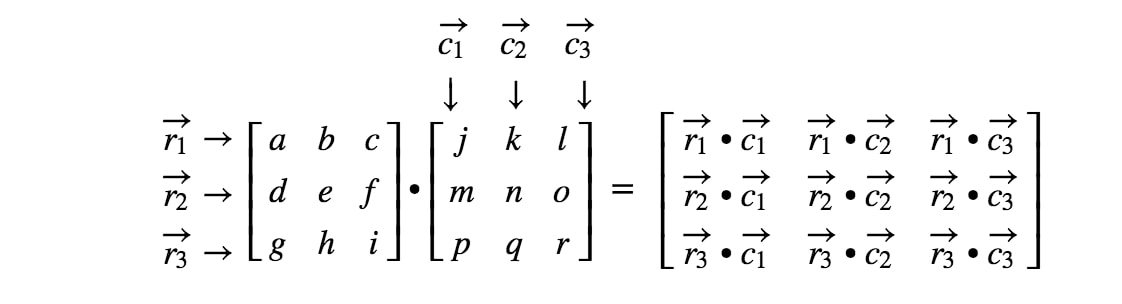
So what was the point of learning the dot product? Well, we will be using the dot product when we multiply two matrices together. When multiplying a matrix with another matrix, we want to treat rows and columns as a vector. More specifically, we want to treat each row in the first matrix as vectors, and each column in the second matrix as vectors. Let's do an example.
Question 3: Find if
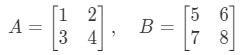
Multiplying the two matrices will give us:
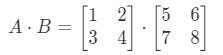
Now the rows and the columns we are focusing are

where is the first row, is the second row, and, are first and second columns. Now we are going to treat each row and column we see here as a vector.
Notice here that multiplying a 2 x 2 matrix with another 2 x 2 matrix gives a 2 x 2 matrix. In other words, the matrix we get should have 4 entries.
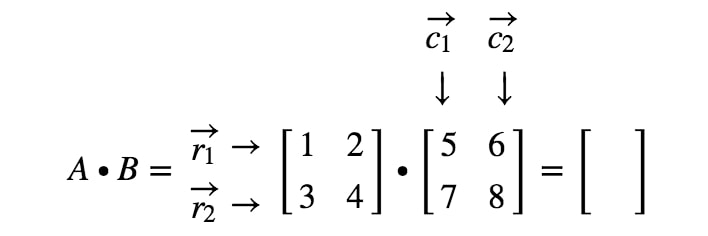
How do we exactly get the first entry? Well, notice that the first entry is located on the first row and first column. So we simply take the dot product of and . Thus, the first entry will be
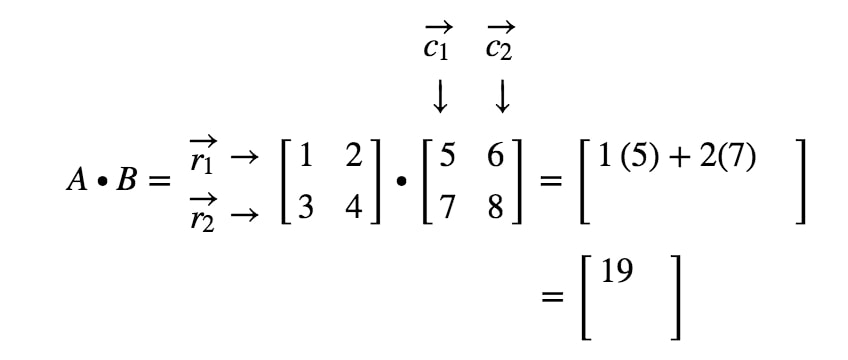
How do we get the second entry this time? Well, notice that the location of the second entry is in the first row and second column. So we simply take the dot product of and . Thus, the second entry will be
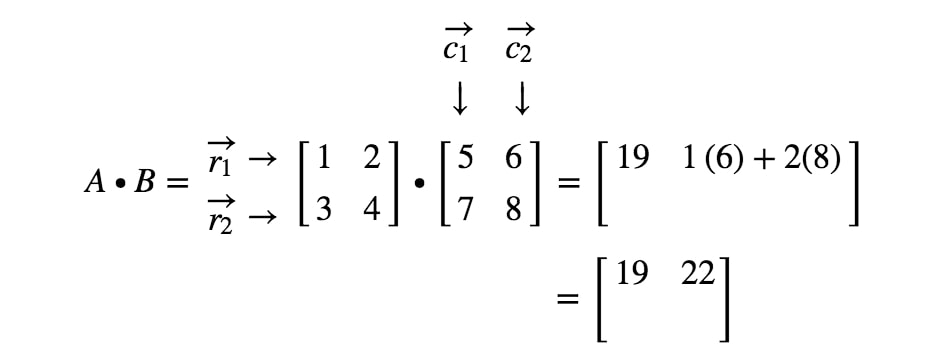
Now we are going to use the same strategy to look for the last two entries. Notice the second last entry is located in the row and column, and the last entry is located in the row and column. So we take the dot product of and , and the dot product of and . This gives us:
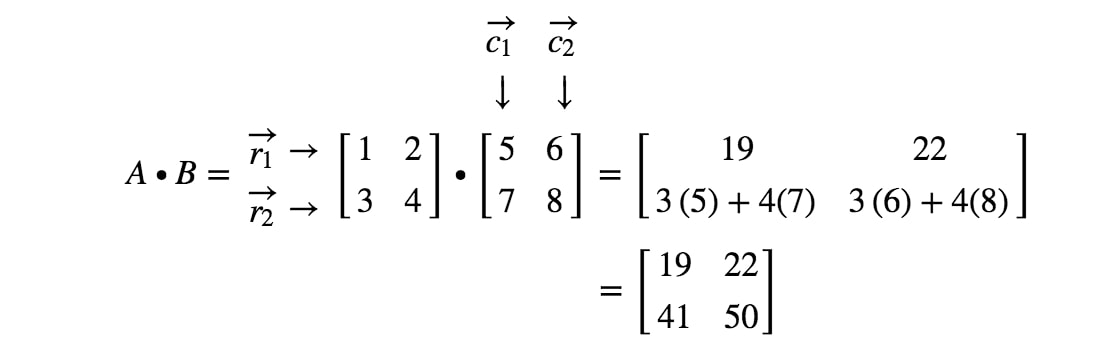
Now we are done! This is what we get when we are multiplying 2 x 2 matrices. In general, the matrix multiplication formula for 2 x 2 matrices is
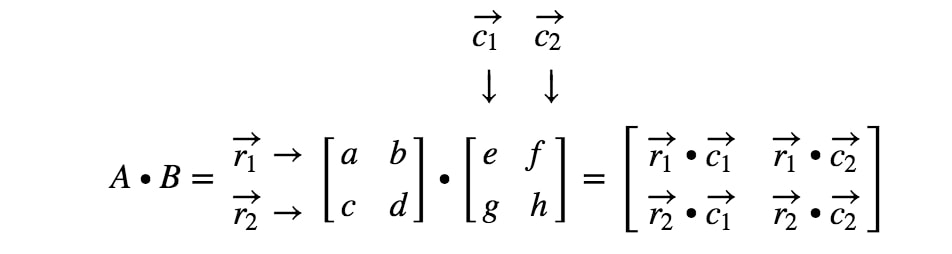
3x3 Matrix Multiplication
Now the process of a 3 x 3 matrix multiplication is very similar to the process of a 2 x 2 matrix multiplication. Again, why don't we do a matrix multiplication example?
Question 4:Find if
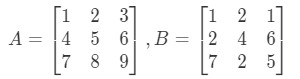
First, notice that multiplying them should give us another 3 x 3 matrix. In other words,
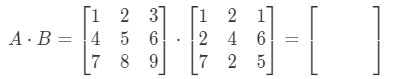
Now let's label all our rows in the first matrix and columns in the second matrix.
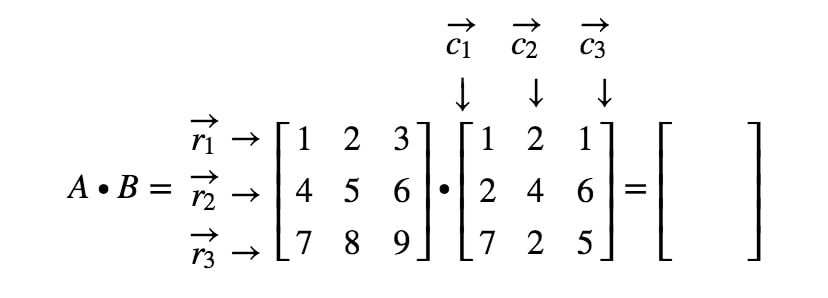
Notice that the first entry of the matrix is located in the row and column, so we take the dot product of and . This gives us:
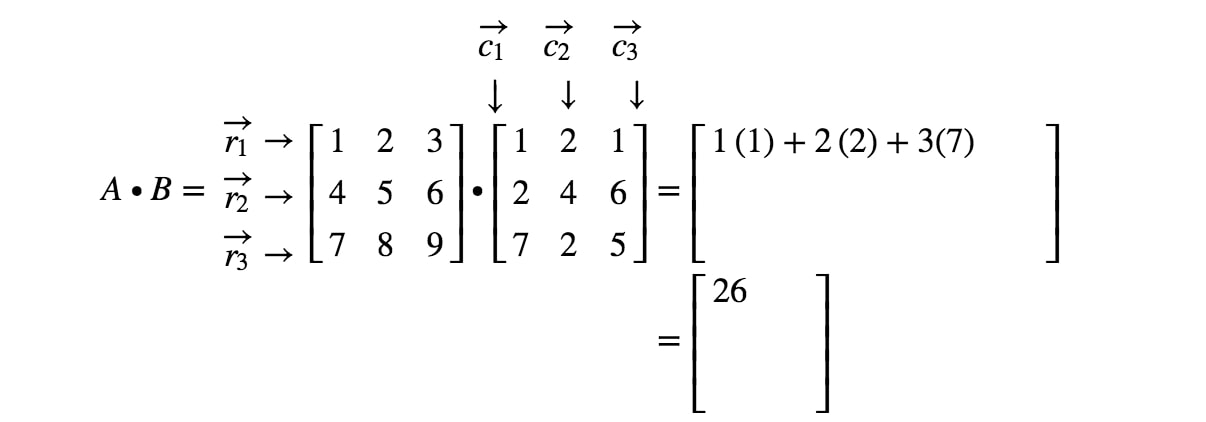
Now notice that the second entry of the matrix is located in the row and column. Thus, we take the dot product of and . This gives us:
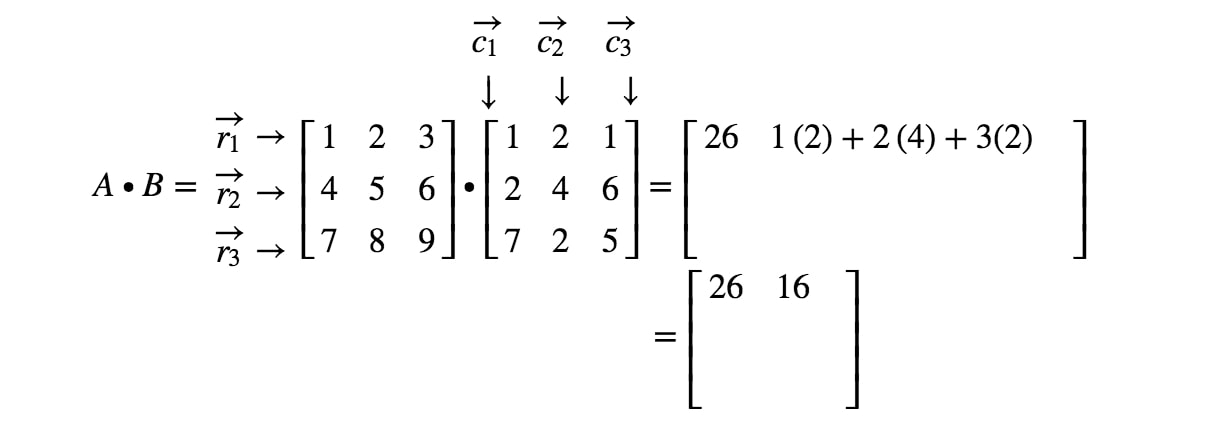
If we are to keep locating all the entries and doing the dot product corresponding to the rows and columns, then we get the final result.

We are done! Notice that the bigger the matrices are, the more tedious matrix multiplication becomes. This is because we have to deal with more and more numbers! In general, the matrix multiplication formula for 3 x 3 matrices is
How to Multiply Matrices with Different Dimensions?
So far we have multiplied matrices with the same dimensions. In addition, we know that multiplying two matrices with the same dimension gives a matrix of the same dimensions. But what happens if we multiply a matrix with different dimensions? How would we know the dimensions of the computed matrix? First, we need to see multiplying the matrices gives you a defined matrix.
Is the Matrix Defined?
There are cases where it is not possible to multiply two matrices together. For those cases, we call the matrix to be undefined. How can we tell if they are undefined?
The product of two matrices is only defined if the number of columns in the first matrix is equal to the number of rows of the second matrix.
Let's try to use this definition in this example.
Question 5: Let
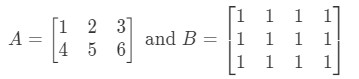
Is defined?
First, notice that the first matrix has 3 columns. Also, the second matrix has 3 rows. Since they are both equal to 3, then I know that is defined.
Now that we know it is defined, how would we know the dimensions of ?
The Dimension Property
To find the dimensions of , we need to first look at the dimensions of and separately.

Now we are going to put the dimensions of the matrices side by side like this:
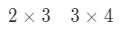
What we are going to do now is take the first number and the last number and combine it to get the dimensions of . See that the first number is 2 and the last number is 4. So the dimensions of will be:
Now that we know the dimensions of the matrix, we can just compute each entry by using the dot products. This will give us:
Now that we know how to multiply matrices very well, why don't take a look at some matrix multiplication rules?
Matrix Multiplication Properties
So what type of properties does matrix multiplication actually have? First, let's formally define everything.
Let be matrices, be an identity matrix, and be a zero matrix. If all five of these matrices have equal dimensions, then we will have the following matrix to matrix multiplication properties:

The associative property states that the order in which you multiply does not matter. In other words, computing and then multiply with would give you the same result as computing and then multiplying with . Let's do an example.
Question 6: Show that the associative property works with these matrices:
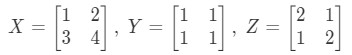
Looking at the left side of the equation in the associative property, we see that gives:
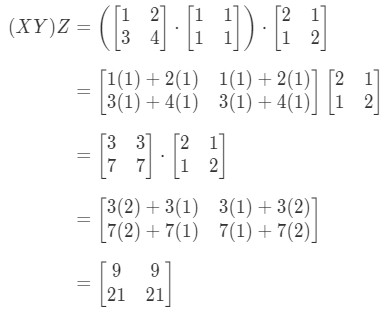
Now looking at the right side of the equation in the associative property, we see that gives:
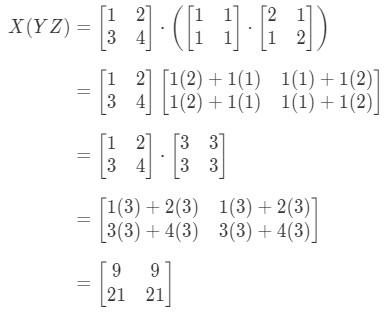
See how the left side and right side of the equation are both equal. Hence, we know that the associative property actually works! Again, this means that matrix multiplication order does not matter!
Now the next property is the distributive property. The distributive property states that:
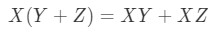
We see that we are allowed to use the foil technique for matrices as well. Just to show that this property works, let's do an example.
Question 7: Show that the distributive property works for the following matrices:
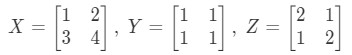
See that the left hand side of the equation is . Hence computing that gives us:
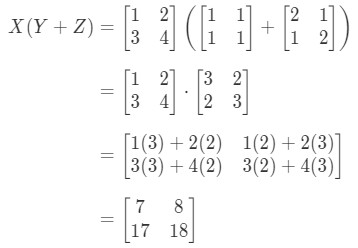
Now let's check if the right hand side of the equation gives us the exact same thing. Notice that the right hand side of the equation is . Computing this gives us:
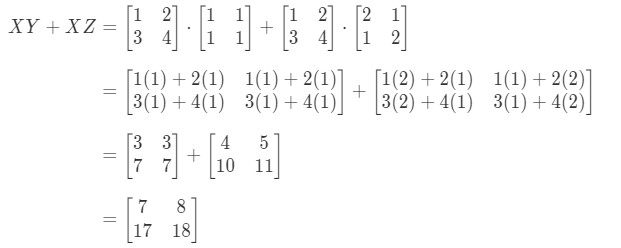
Notice that the left hand side of the equation is exactly the same as the right hand side of the equation. Hence, we can confirm that the distributive property actually works.
Is Matrix Multiplication Commutative?
We know that matrix multiplication satisfies both associative and distributive properties, however we did not talk about the commutative property at all. Does that mean matrix multiplication does not satisfy it? It actually does not, and we can check it with an example.
Question 8: If matrix multiplication is commutative, then the following must be true:
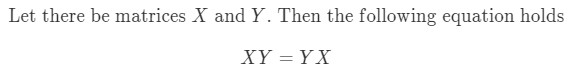
Show that if
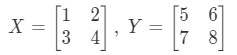
First we compute the left hand side of the equation. Calculating gives us:
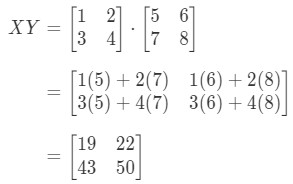
Now computing the right hand side of the equation, we have:
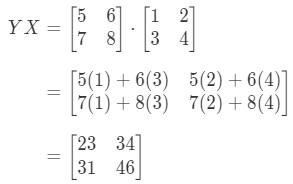
As you can see,
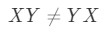
Because we have
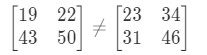
These two matrices are completely different.
Now there are still a few more properties of the multiplication of matrices. However, these properties deal with the zero and identity matrices.
Matrix Multiplication for the Zero Matrix
The matrix multiplication property for the zero matrix states the following:
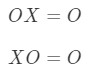
where is a zero matrix.
This is means that if you were to multiply a zero matrix with another non-zero matrix, then you will get a zero matrix. Let's test if this is true with an example.
Question 9: Show that the equation and holds if:
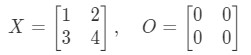
Let's first look at the equation
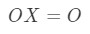
Notice that calculating gives us:
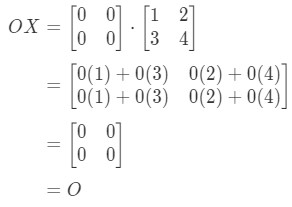
We do see that , so the equation holds. Similarly, if we calculate , we get:
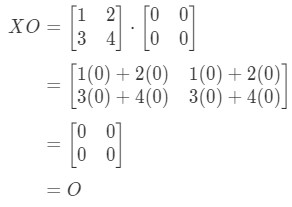
We do see that the equation holds, so we are done.
Matrix Multiplication for the Identity Matrix
Now what about the matrix multiplication property for identity matrices? Well, the property states the following:
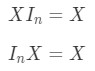
where is an identity matrix. Again, we can see that the following equations do hold with an example.
Question 10: Show that the equations and holds with the following matrices
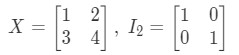
So for the equation , we have:
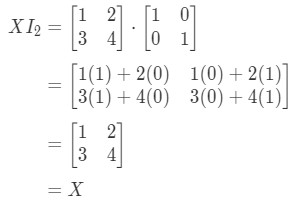
So the equation does hold. Similar to the equation , we have:
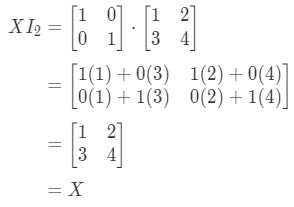
Again, the equation holds. So we are done with the question, and both equations hold. This concludes all the properties of matrix multiplication. Now if you want to look at a real life application of matrix multiplication, then I recommend you look at this article.
https://www.mathsisfun.com/algebra/matrix-multiplying.html
A -tuple is an ordered list of numbers. For example,
(1,2,3,4) is an ordered quadruple with 4 numbers, and (1,2,3) is an ordered triple with 3 numbers. We usually specify each ordered -tuple as a variable with an arrow on top. For example,
If we have 2 ordered -tuples, then we can find the dot product. The dot product is summation of all the product of each corresponding entries. For example, let
and .
If we do the dot product of and and ,then we will get the following:
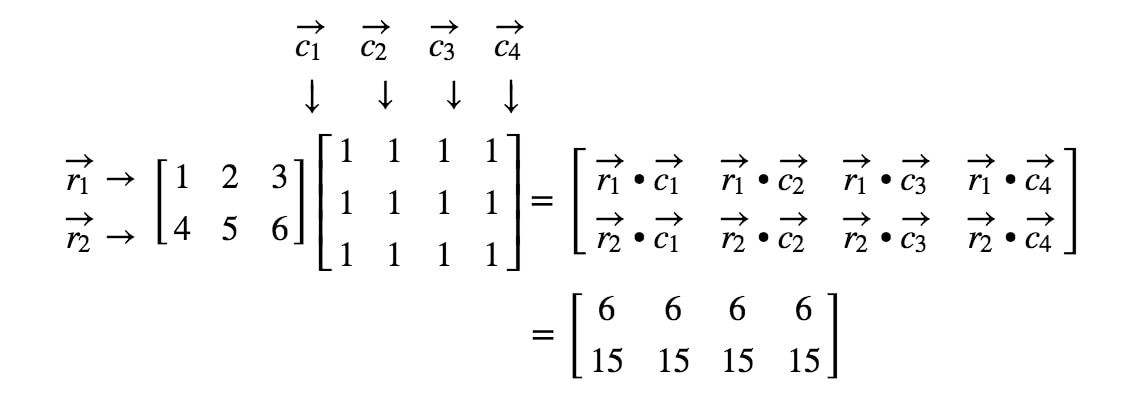
When we want to multiply a matrix by a matrix, we want to think of each row and column as a -tuple. To be exact, we want to focus on the rows of the first matrix and focus on columns of the second matrix. For example,
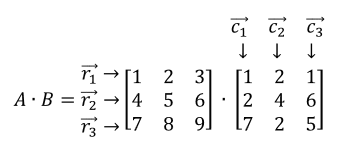
For example, is the first row of the matrix with an ordered triple (1,2,3). Now to multiply these two matrices, we need to use the dot product of to each column, dot product of to each column, and to each column. In other words