The principle of inclusion and exclusion of 3 sets says the following:
Mastering Intersection and Union of 3 Sets Unlock the power of set theory with our comprehensive guide on intersection and union of 3 sets. Learn essential formulas, visualize concepts with Venn diagrams, and apply your skills to real-world problems.
Get the most by viewing this topic in your current grade. Pick your course now.
- Finding Intersection and Union of 3 Sets
The Venn Diagram below shows the type of instruments that people like.
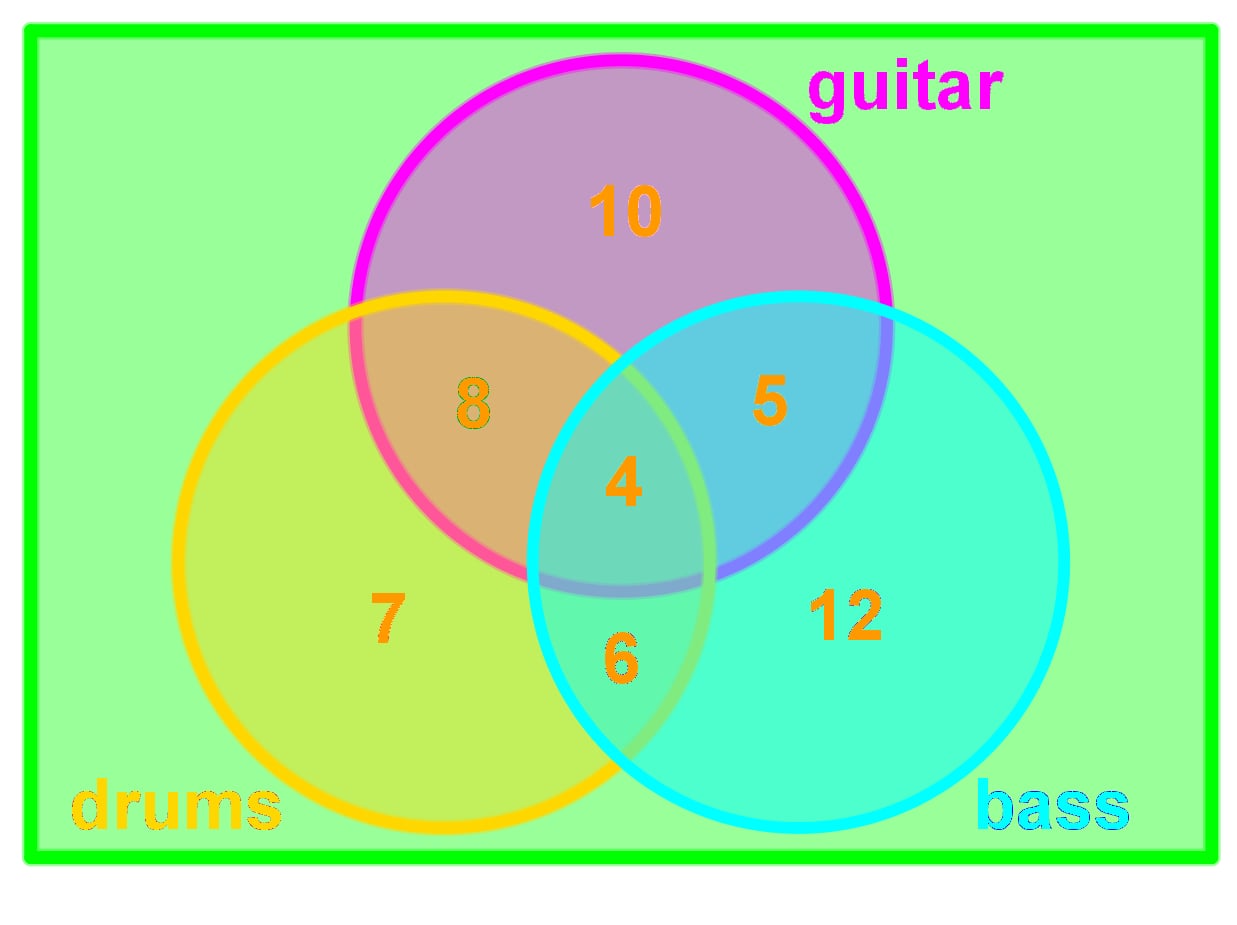
Find the following:
- Given the following Venn diagram:
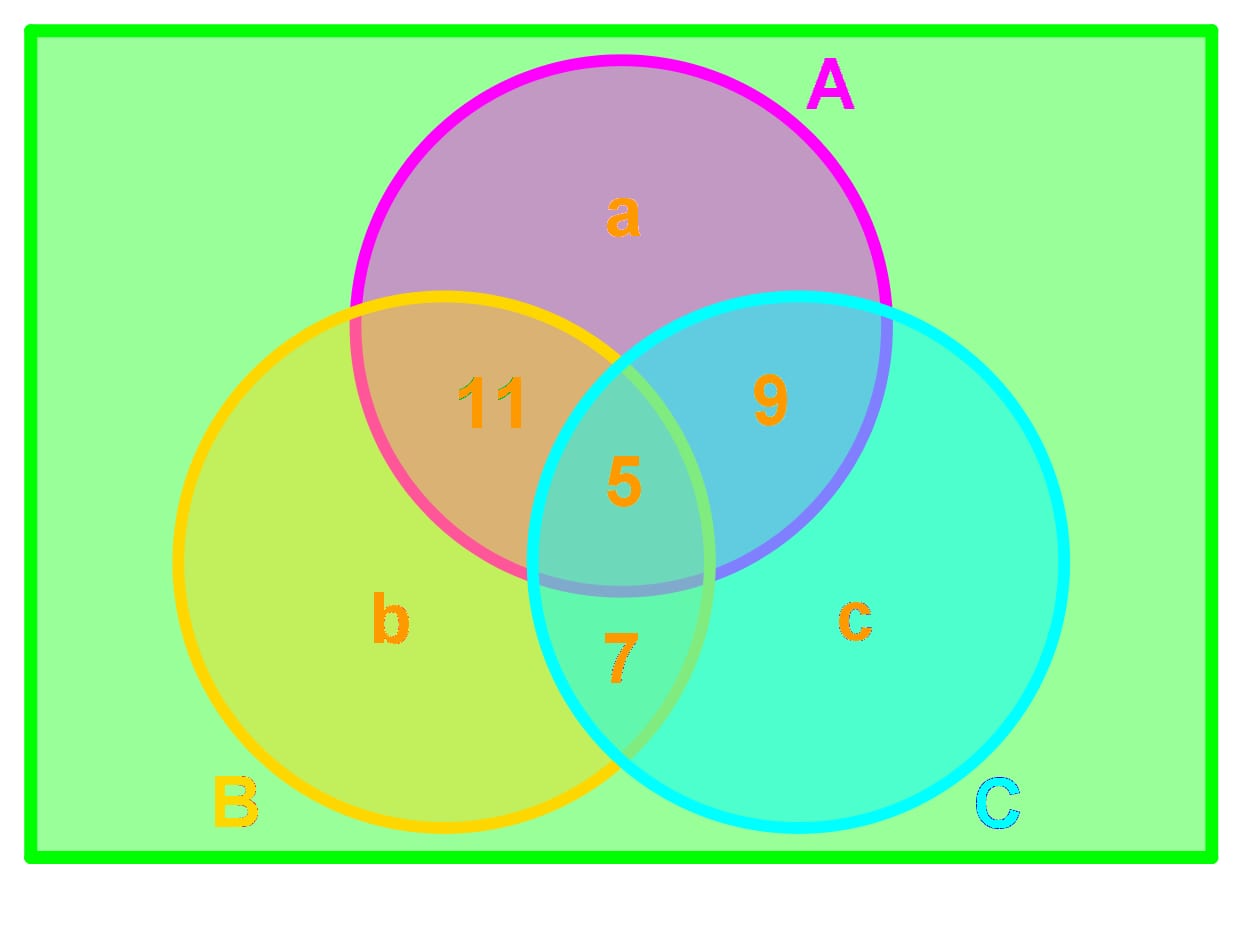
Circle and contain the same number of element. Find and .
- Richard surveyed 200 people to see which sports they like. Here is the information that Richard got:
- 70 people like soccer.
- 60 people like basketball.
- 50 people like tennis.
- 25 people like soccer and basketball, but not tennis
- 10 people like soccer and tennis, but not basketball.
- 7 people like basketball and tennis, but not soccer
- 10 people like all three sports
How many people don't like any of the sports?
- Principle of Inclusion and Exclusion with 3 Sets
Willy surveyed 76 people for a cake shop. Each person ate at least one of the cakes: strawberry, chocolate and vanilla. Here is the information Willy got:
- 57 ate strawberry, 50 ate chocolate, and 39 ate vanilla.
- 20 ate both strawberry and chocolate, but not vanilla.
- 15 ate strawberry and vanilla, but not chocolate.
- 5 ate chocolate and vanilla, but not strawberry.
Who ate all three types of cakes?






