Introduction to Volume: Understanding 3D Shapes Dive into the world of volume calculations. Learn to measure 3D shapes, apply formulas, and solve real-world problems. Enhance your spatial reasoning and geometry skills with our comprehensive guide.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
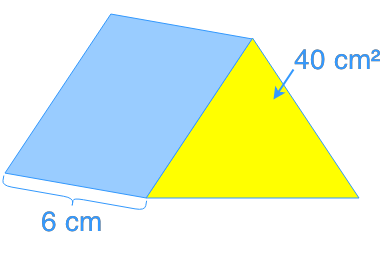
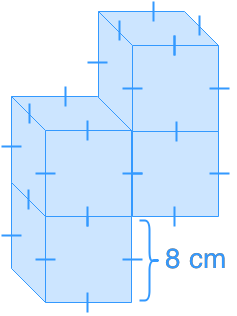
Introduction to Volume
Volume is a fundamental concept in mathematics that measures the amount of space occupied by a three-dimensional object. This lesson introduces volume calculations for 3D shapes, building upon your previous knowledge of surface area to volume. The accompanying introduction video serves as a crucial resource, providing a visual and interactive approach to understanding volume. We'll explore how to calculate the volume of various 3D shapes, focusing particularly on triangular prisms and cylinders. These shapes are common in everyday life and engineering applications, making this knowledge both practical and essential. By mastering volume calculations, you'll gain a deeper appreciation for spatial relationships and enhance your problem-solving skills in geometry. The transition from surface area to volume represents a significant step in your mathematical journey, opening doors to more advanced concepts in three-dimensional geometry and spatial reasoning.
-
What is the difference between volume and capacity?
Volume refers to the amount of space occupied by a three-dimensional object, while capacity is the amount of substance an object can hold. For example, a bottle may have a volume of 500 cubic centimeters, but its capacity might be listed as 500 milliliters. In many cases, especially with liquids, 1 milliliter is equivalent to 1 cubic centimeter, making the conversion straightforward.
-
How do you calculate the volume of a cylinder?
To calculate the volume of a cylinder, use the formula V = πr²h, where r is the radius of the circular base and h is the height of the cylinder. First, identify the radius and height, then square the radius, multiply by pi (π), and finally multiply by the height. For example, if a cylinder has a radius of 3 cm and a height of 8 cm, its volume would be V = π × 3² × 8 226.19 cm³.
-
Why is the volume formula for a pyramid different from a prism?
The volume formula for a pyramid (V = 1/3 × B × h) includes a factor of 1/3, unlike the formula for a prism (V = B × h). This is because a pyramid tapers to a point, resulting in a volume that is exactly one-third of a prism with the same base area and height. The tapering shape means that as you move from the base to the apex, the cross-sectional area gradually decreases, unlike in a prism where it remains constant.
-
How can I avoid common mistakes when calculating volume?
To avoid common mistakes in volume calculations: 1) Always identify the correct formula for the specific shape. 2) Ensure all measurements are in the same units before calculating. 3) Double-check your work, especially when dealing with complex shapes. 4) For irregular shapes, try breaking them down into simpler geometric forms. 5) Use estimation to check if your final answer makes sense within the context of the problem.
-
What are some real-world applications of volume calculations?
Volume calculations have numerous real-world applications. In architecture, they're used to design efficient spaces and optimize acoustics. Engineers use volume calculations for material estimation in construction and fluid dynamics in machinery design. In manufacturing, volume calculations are crucial for mold design and product packaging. Even in daily life, we use volume concepts in cooking, gardening, and home improvement projects. Understanding volume is essential in fields ranging from medicine (for dosage calculations) to environmental science (for water resource management).
Understanding the concept of volume is crucial in mathematics and real-world applications. To fully grasp the introduction to volume, it's essential to have a solid foundation in several prerequisite topics. These topics provide the necessary background knowledge and skills to comprehend volume calculations and their practical uses.
One of the key prerequisites is understanding the surface area and volume of cones. This topic introduces the concept of three-dimensional shapes and how to calculate their volume. It also helps in understanding the relationship between surface area and volume, which is fundamental when dealing with more complex shapes.
Another important prerequisite is conversions involving squares and cubic units. This knowledge is crucial for accurately measuring and expressing volume in different units. Being able to convert between various cubic units allows for better comprehension and application of volume concepts in diverse contexts.
Mastering volume of rectangular prisms word problems is also essential. This topic helps develop problem-solving skills and the ability to apply volume calculations to real-world scenarios. It bridges the gap between theoretical knowledge and practical applications, making the concept of volume more tangible and relevant.
Additionally, understanding the volume of prisms, particularly triangular prisms, is crucial. This knowledge expands on the concept of volume for different shapes and helps in recognizing patterns and relationships between various three-dimensional objects.
By mastering these prerequisite topics, students will be better equipped to tackle more advanced volume concepts. They will have a strong foundation in calculating volumes of different shapes, converting between units, and applying these skills to solve real-world problems. This comprehensive understanding will make the introduction to volume more accessible and meaningful.
Moreover, these prerequisites are interconnected. For instance, the knowledge of surface area and volume of cones can be applied to understand the volume of other shapes like cylinders. Similarly, the ability to solve word problems involving rectangular prisms can be extended to more complex shapes and real-life situations.
In conclusion, a thorough grasp of these prerequisite topics is vital for a smooth transition into more advanced volume concepts. They provide the necessary tools and understanding to approach volume calculations with confidence and accuracy. By building on this foundation, students will be well-prepared to explore more complex aspects of volume and its applications in various fields of study and everyday life.